Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 44
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-48
44. Cicloide , no intervalo:
a.
b.
c.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Nesse caso, estamos falando de um cicloide, com as equações paramétricas fornecidas no enunciado, no intervalo , com isso, temos que
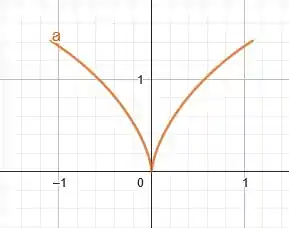
Passo 2
B – Para o intervalo
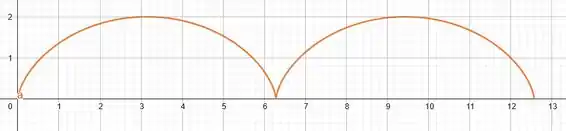
Passo 3
C – Já no intervalo de
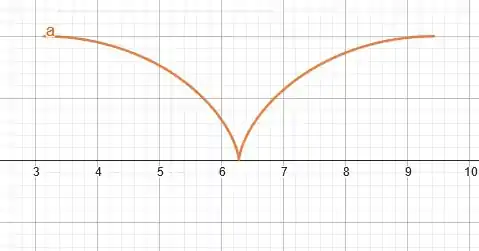
Resposta
Respondido acima!
Exercícios de Livros Relacionados
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-4841. Elipse - x = 4 cos t ,y = 2 sen
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-48Uma curva interessante - x = 3 cos t
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-4843. Parábola x = 2 t + 3 ,y = t 2 - 1
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-4847. a. Epicicloide x = 9 cos t - cos
Encontre uma parametrização para a curva y = x com ponto final ( 0,0 ) utilizando o ângulo u na figura a seguir como parâmetro.