Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 73
Use o método descrito no exercício 71.
Esboce o gráfico de
(a)
(b)
Passo 1
(a) Bom, o enunciado do exercício 71 já nos diz todo o raciocínio da questão. Pois ele explica que o gráfico da função módulo () pode ser obtido a partir do gráfico da função dentro do módulo (), mantendo iguais os valores acima de , mas refletindo pelo eixo todos os valores que estão abaixo desse eixo.
Dessa forma, vamos usar o mesmo raciocínio, o lance é que e, então, . Ok? Então, vamos mexer apenas na parte do gráfico de que está abaixo do eixo , pois vamos refletir essa parte pelo eixo .
Passo 2
O gráfico de é:
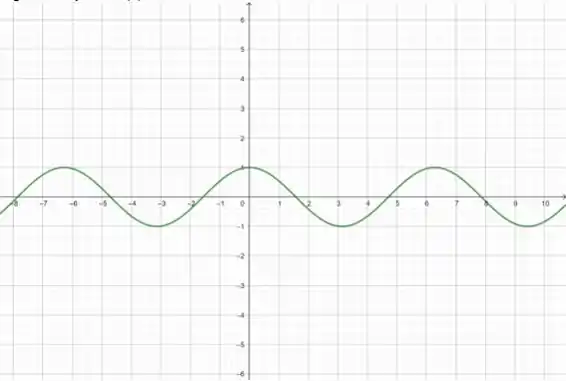
Perceba os valores abaixo do eixo ! Vamos refletir esses valores em torno do eixo :
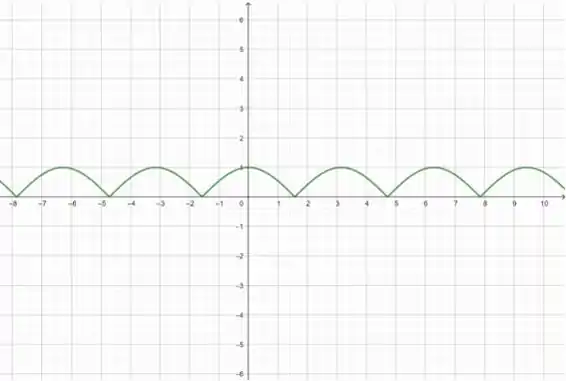
Viu? É só isso! Esse é o gráfico de .
Passo 3
(b) Então, para esboçar o gráfico, vamos somar os gráficos de e . Para isso, basta imaginar que eles estejam “empilhados” um em cima do outro. Vamos ver isso melhor.
Primeiro, o gráfico de :
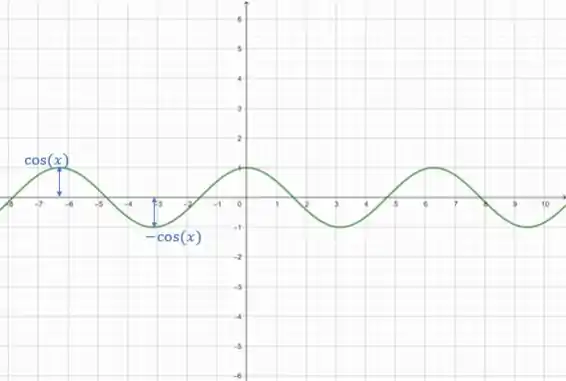
Agora, vamos desenhar o no mesmo sistema:
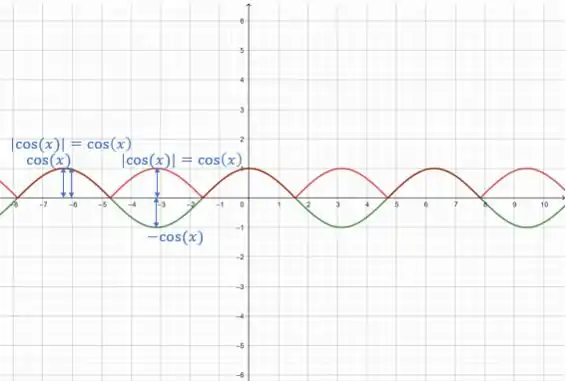
Podemos ver que teremos partes em que os gráficos se somam e outras em que eles se cancelam, tendo um parte positiva com uma negativa ()! Onde elas se somam, teremos o dobro do gráfico, pois fica .
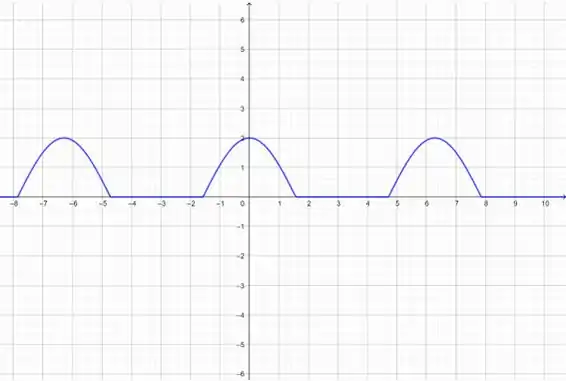
Dessa forma, o gráfico de (em azul):
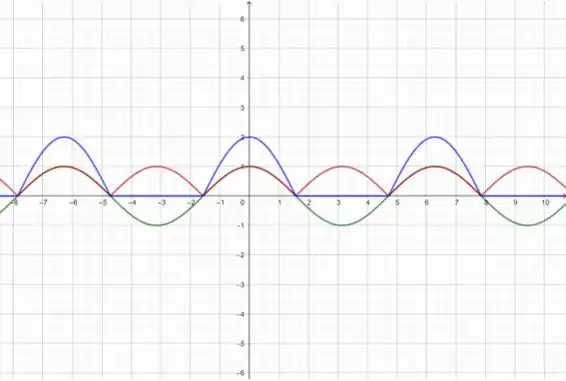
Beleza? Agora, vamos colocar só o gráfico que nos interessa:
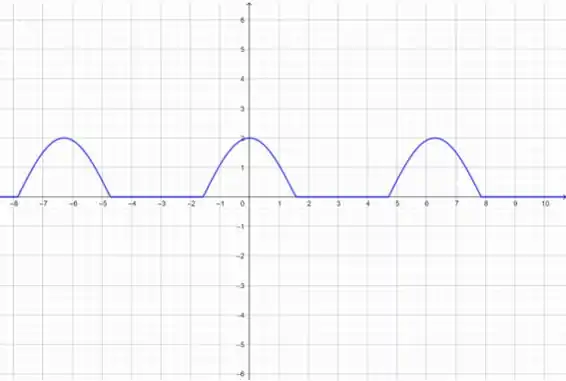
Resposta
(a)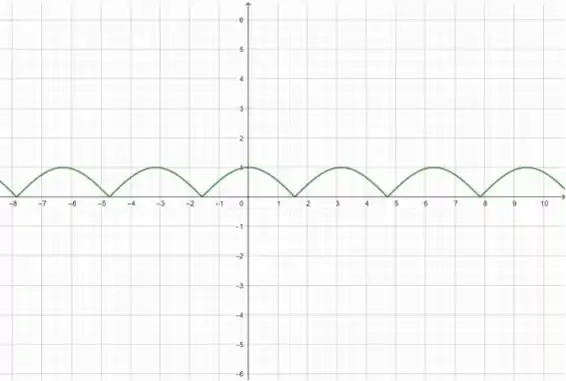 
(b) 