(a) Esboce o gráfico de adicionando as correspondentes coordenadas y nos gráficos de y = x e y = |x|.
(b) Expresse a equação na forma por partes, sem valores absolutos e confirme que o gráfico obtido em (a) com essa equação é consistente.
Passo 1
(a) Então, para esboçar o gráfico, vamos somar os gráficos de e . Para isso, basta imaginar que eles estejam “empilhados” um em cima do outro. Vamos ver isso melhor.
Primeiro, o gráfico de :
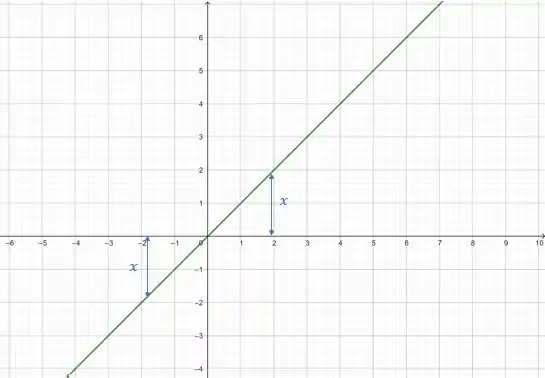
Agora, vamos desenhar o no mesmo sistema:
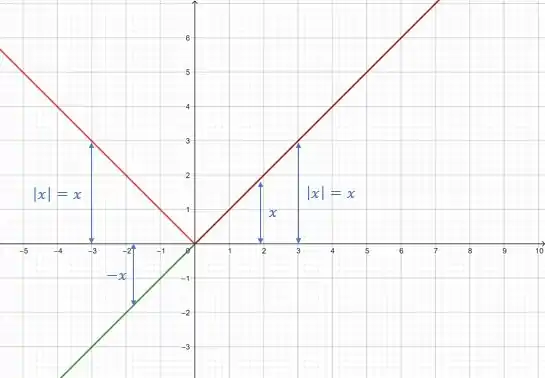
Bom, a distância do eixo até um ponto em é igual a distância do eixo ao . Isso falando de um mesmo ponto, por exemplo , que aí seria a distância de até e até , ou seja, é a distância do eixo até o mesmo ponto.
Com isso, para achar a soma das duas, vamos somar os valores de cada : na parte positiva do eixo , temos que as duas funções possuem valores positivos, então, vai aparecer algo acima delas, pois ocorrerá uma soma de valores positivos!
Já na parte negativa do eixo , os valores da função são negativos (repare ali o )! Enquanto de continuam positivos. Logo, esses valores vão se subtrair, pois um será positivo e o outro será negativo... Assim, aparece algo entre as duas funções, nesse lado do gráfico.
Como já vimos que, para um mesmo ponto em , os valores de e serão iguais, na soma (parte positiva de ), teremos um gráfico com o dobro dos valores das funções. Já na subtração (parte negativa de ), teremos um cancelamento dos valores das funções, o que dará um valor até a origem.
Dessa forma, soma das duas vai aparecer assim (em azul):

Como falamos, os valores ao lado direito de estão dobrados e os valores ao lado esquerdo, são nulos!
Agora, só o gráfico que nos interessa:
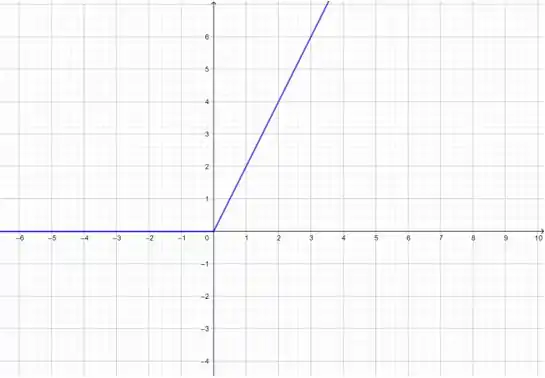
Esse é o gráfico de .
Passo 2
(b) Esquece o gráfico que vimos, por enquanto, e vamos escrever por partes.
Sabemos que é para e para , isso porque o módulo vai transformar todos os valores de para valores positivos, então temos que inverter o sinal quando e quando não precisamos mudar nada, pois o valor já é positivo. Então temos:
Para :
Para :
A diferença é que agora vamos adicionar um nessa equação. Então:
Para :
Para :
Juntando essas informações, podemos escrever a função assim:
Opa, é exatamente o que achamos na letra anterior:
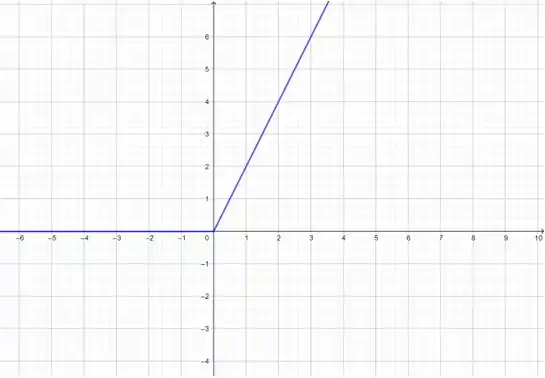
Repare que para , nossa função era nula e para , vimos que os valores haviam dobrado, ou seja, viraram .
Resposta
(a) 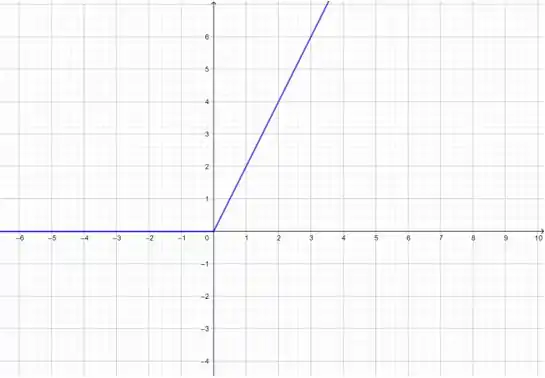
(b) Bateu!