Esboce o gráfico da equação por translação, reflexão, compressão e alongamento do gráfico de , , , ou de maneira apropriada e, então, use um recurso gráfico para confirmar que seu esboço está correto.
Passo 1
Bem, nessa questão, nós vamos usar os princípios de translação, alongamento, compreensão e reflexão vistos nesse capítulo e que ficaram bem resumidos na tabela 0.2.2, 0.2.3 e 0.2.4.
Basicamente:
Se temos uma função, por exemplo, e somamos uma constante positiva à função, por exemplo , deslocamos o gráfico da função na quantidade equivalente ao valor da constante para cima (no nosso exemplo, deslocaríamos em 1 unidade para cima no eixo ).
Se subtraímos uma constante à função (), deslocamos o gráfico para baixo (no exemplo, seria 1 unidade para baixo no eixo ).
Se somamos uma constante positiva ao (ex.:), deslocamos o gráfico para a esquerda (no exemplo, seria 1 unidade para a esquerda no eixo ).
Se subtraímos uma constante positiva ao (ex.:), deslocamos o gráfico para a direita (no exemplo, seria 1 unidade para a direita no eixo ).
Se multiplicamos a função por uma constante positiva maior que , alongamos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos a função por uma constante positiva entre e , comprimimos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos por uma constante positiva maior que , comprimimos o gráfico no eixo horizontal por um fator equivalente à constante.
Se multiplicamos por uma constante positiva entre e , alongamos o gráfico no eixo horizontal por um fator equivalente à constante.
Se substituímos por , refletimos o gráfico pelo eixo .
Se multiplicarmos a função por , refletimos o gráfico pelo eixo .
Vamos usar esses conceitos para resolver essa questão!!
Passo 2
Olhando para a função:
Bem, ela não está do jeito que estamos acostumados né? Então, vamos só arrumar um pouquinho ela, passando o termo com para o outro lado:
Agora sim! E vemos que temos um no dentro de uma raiz cúbica, certo? Então, se assemelha mais ao .
Passo 3
Vamos identificar as modificações partindo de :
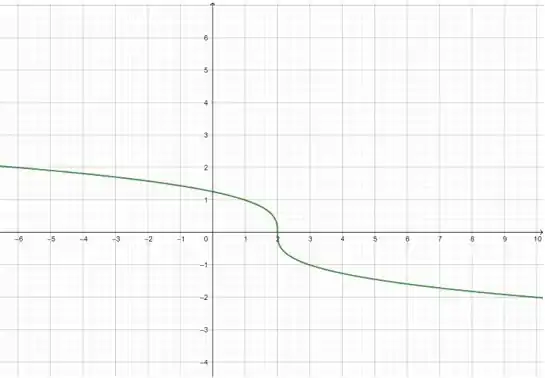
Primeiro, subtraímos 2 ao , o que desloca o gráfico de em 2 unidades para direita:
Passo 4
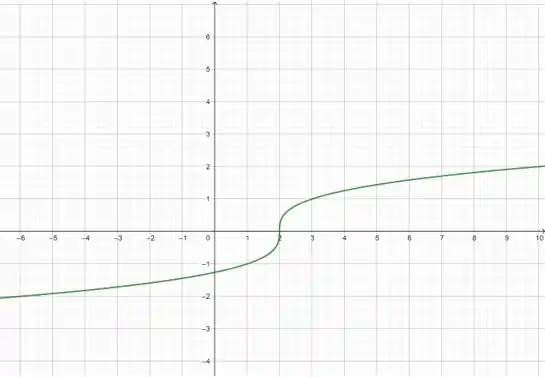
Agora, temos . O próximo passo é multiplicar a função por , o que reflete o gráfico pelo eixo :
Com isso, chegamos no gráfico de .
Resposta