Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 22
Use o método de Euler com o passo para estimar onde é a solução do problema de valor inicial
Passo 1
Para resolver esse problema vamos precisar lembrar como funciona o Metodo de Euler. Esse método nos fornece um caminho de resolver equações diferenciais de uma forma numérica. Podemos escrever a equação de Euler como
Onde nosso
E também
Passo 2
Agora que já demos aquela relembrada básica, podemos cair dentro. (Caso você tenha alguma duvida sobre a parte mais teórica sobre o método de Euler, temos uma seção em nosso site que vai te explicar passo a passo como ela é construída. : D ). Vamos agora usar nossos dados para resolver o problema
Isso quer dizer que
Então nosso fica :
Show! Fizemos um passo a passo de como funciona para construir nossa sequência de dados, vamos montar uma tabela com os próximos valores de
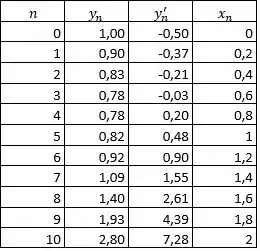
Com isso podemos plotar o seguinte gráfico
Quanto menor for o incremento em x melhor será a aproximação numérica do Metodo de Euler. Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)