Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 7
Encontre o vértice, o foco, e a diretriz da parábola e esboce o seu gráfico.
Passo 1
Falaee, belezinha?? Bom... o enunciado nos dá a seguinte equação que descreve uma parábola:
Queremos encontrar o vértice, o foco e a diretriz dessa parábola... mas o que são eles?
Bom... seja a seguinte parábola:
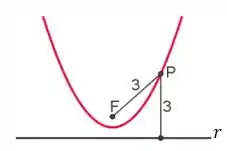
- O ponto é chamado de foco e determina essa figura;
- A reta é chamada de diretriz da parábola. A distância entre qualquer ponto da parábola e a sua diretriz é igual à distância entre esse mesmo ponto da parábola e o seu foco;
- O vértice da parábola é o ponto mais próximo de sua diretriz.
Para encontrarmos o foco e a diretriz, temos que encontrar o valor de na seguinte equação padrão da parábola:
E, para encontrarmos o vértice, basta reorganizar a equação dada e ver os números que estão somando ou subtraindo os valores de e .
Então bora lá!! 😉
Passo 2
Vamos encontrar o valor de organizando a equação dada:
Somando nos dois lados:
Completando quadrado do lado direito e tirando fator comum do lado direito:
Agora através da equação padrão da parábola:
Podemos comparar o termo que multiplica os parênteses da equação com o lado direito da equação acima, p será:
Passo 3
Logo, o foco que é dado por será
E a diretriz pode ser obtida pela equação:
Repare que somamos as translações nas definições de foco e de diretriz, pois elas são dadas no livro para uma parábola que NÃO está transladada.
Passo 4
Para obtermos o vértice, precisamos olhar para a equação do passo 2 que obtemos:
Assim, os termos que estão subtraindo a e a (caso seja uma soma, nós invertemos o sinal) na equação serão as coordenadas do ponto.
Então comparando, podemos concluir que o vértice será .
Resposta
Foco:
Diretriz:
Vértice: