Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 32
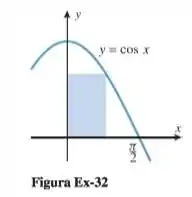
Use o Método de Newton para aproximar as dimensões do retângulo de maior área que pode ser inscrito sob a curva , conforme a Figura Ex-32.
Passo 1
Fala aí! Tudo joia?
Bom, a área de um retângulo é , onde são as dimensões dele. Até aí nada de novidade.
A questão aqui é relacionar essa área com a função. Repare o seguinte: . Ou seja, nossa área pode ser calculada fazendo:
É essa função que a gente quer maximizar. Então bora!
Passo 2
A gente tem que derivar, pra começo de conversa:
Beleza, pra saber onde isso zera a gente vai ter usar o método de Newton.
Vamos colocar e achar uma aproximação para:
Passo 3
Para usar o método de Newton, a gente faz:
Beleza, achamos esse valor aproximado onde a derivada zera.
Passo 4
Pra verificar que é máximo, é só jogar na derivada segunda da função:
Logo, é ponto de máximo.
E aí é só a gente ver a dimensão agora:
Prontinho! Essas são as aproximações das dimensões do retângulo pedido😉