Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 34
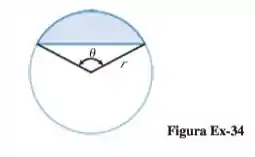
Um segmento de um círculo é a região compreendida por um arco e sua corda (ver Figura Ex-34). Se for o raio do círculo θ , o ângulo subentendido no centro do círculo, então pode-se mostrar que a área A do segmento é , onde está em radianos. Encontre o valor de para o qual a área do segmento é um quarto da área do círculo. Dê o valor de até o grau mais próximo.
Passo 1
Fala aí! Tudo joia?
Olha só: a gente quer que a área seja igual a um quarto da área do círculo. Um quarto da área do círculo é certo? Então a gente quer isso aqui:
Agora a gente dá uma simplificada...
A gente precisa achar uma raiz pra essa equação aí então.
Passo 2
A gente vai ter que usar o tal do método de Newton pra achar uma raiz aproximada aí.
Para usar o método de Newton, a gente faz:
Vamos precisar derivar:
A raiz disso tá ali entre (dá pra ver se olhar no gráfico da função).
Então a gente vai usar .
Passo 3
Então a gente joga na fórmula agora:
Então a aproximação do ângulo em radianos é aproximadamente . Em graus então é aproximadamente 😽