Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 32
- Use o método de Newton com para encontrar a raiz da equação com precisão de seis casas decimais.
- Resolva a equação da parte (a) usando como aproximação inicial .
- Resolva a equação da parte (a) utilizando . (Você definitivamente precisa de uma calculadora programável para esta parte.)
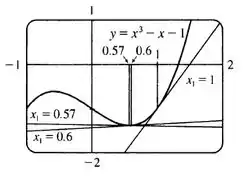
- Faça o gráfico de e suas retas tangentes em , e para explicar por que o método de Newton é tão sensível ao valor da aproximação inicial.
Passo 1
Oie, meu amigo. Vamos resolver essa atividade juntos hoje.
Temos a equação:
E iremos utilizar o método de Newton para encontrar as equações dessa equação.
Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:
Em que e por assim diante é a nossa raiz, o que fazemos é dado um valor para a candidata a ser a raiz, nós vamos desenvolvendo diversos até não encontrarmos mais variações significativas de valores.
Parece confuso, mas durante o desenvolvimento você irá entender melhor.
Primeiro passo é derivar a nossa que será a:
Depois disso nos é dado que , e então iremos procurar as raízes em diante.
Passo 2
- Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:
- Para achar a raiz usando a aproximação inicial vamos então para os nossos repetidos cálculos:
- A questão aconselha a usar uma calculadora programável, pois aqui a gente teria que fazer VARIOS cálculos para encontrarmos a raiz, então vamos nos preparar, vamos fazer no mesmo esquema da letra (b), usando :
- Aqui temos o gráfico de e suas retas tangentes em , e :
Primeiro temos que
Vamos agora precisar de , vamos calcular então!!
Para achar a derivada de vamos usar algumas regras de derivação, o da função constante e do polinômio:
Vamos calcular :
Passo 3
Pronto, agora que temos é só jogar na fórmula de Newton:
Vamos agora usar como pedido da questão, vamos l��:
Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Ainda está variando, vamos agora com :
Agora com :
Pronto, o valor não varia mais, então a raiz é .
Passo 4
Continuamos usando o Método de Newton até termos duas aproximações que correspondem a até seis casas decimais.
Vamos continuar então, temos que encontrar a precisão pedida.
Agora mais uma:
Outra vez, estamos muito longes:
Veja que por termos começado longe da raiz aproximada, nossa tarefa fica extensa:
Outra vez:
E lá vamos nós:
Outra vez:
Vamos novamente:
Falta pouco:
É a última:
Passo 5
Passo 6
Devo te lembrar que a equação da reta tangente a uma função é dada por:
E é a inclinação da reta tangente, a gente acha ela derivando a nossa função:
O valor dela nos pontos de são:
Agora precisamos encontrar os valores de que são os valores de quando nossa função passa por esses pontos:
Assim nossas retas serão:
Para :
Para :
E para :
Agora vamos plotar nosso gráfico com as retas e a função, iremos utilizar o GeoGebra para isso:
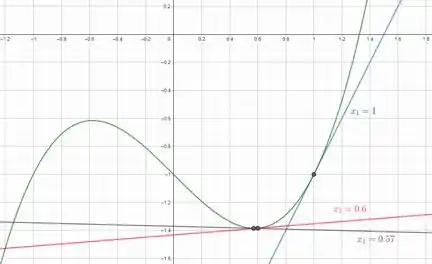
Vamos analisar a figura, a linha tangente corresponde a , que resulta em uma sequência de aproximações que converge muito rapidamente, fazendo .
A linha tangente correspondente a está quase horizontal, então está bem londe da raiz, porém essa sequência ainda converge, só que um pouco mais devagar, fazendo .
Por último, a linha tangente correspondente a é quase horizontal, está mais distante da raiz e por isso temos mais iterações para poder convergir, chegando a .
Resposta
- A raiz é
- A raiz é
- A raiz é
