Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 49

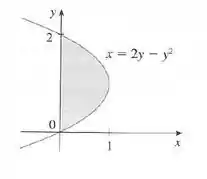
A área da região que está à direita do eixo y e à esquerda da parábola x = 2 y - y 2 (a região sombreada na figura) é dada pela integral ∫ 0 2 2 y - y 2   d y . (Gire sua cabeça no sentido horário e imagine a região como estando abaixo da curva x = 2 y - y 2 de y = 0 até y = 2 .) Ache a área da região.

Passo 1

Essa questão já nos deu pronta a integral para achar a área da região, vamos achar o seu valor então.

A = ∫ 0 2 2 y - y 2   d y = ∫ 0 2 2 y   d y + ∫ 0 2 - y 2   d y

Vamos primeiro calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:

∫ 2 y - y 2   d y = ∫ 2 y   d y + ∫ - y 2 d y

Passo 2

Agora é fácil achar as primitivas de cada função, usando duas expressões da Tabela de Integrais Indefinidas:

∫ c f x d x = c ∫ f x d x

∫ x n d x = x n + 1 n + 1 + C   n ≠ - 1

Agora é só aplicar, vamos resolver elas separadamente, assim fica mais simples de ver:

∫ 2 y   d y = 2 ∫ y   d y = 2 ∙ y 1 + 1 1 + 1 = 2 y 2 2 = y 2 + C

∫ - y 2 d y = - 1 ∫ y 2 d y = - 1 ∙ y 2 + 1 2 + 1 = - y 3 3 + C

Passo 3

Pronto, já encontramos a integral indefinida, perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:

∫ a b f x d x = F b - F a

Ficamos então com:

A = ∫ 0 2 2 y   d y + ∫ 0 2 - y 2   d y = y 2 0 2 + - y 3 3 0 2 = 2 2 - 0 2 + - 2 3 3 - - 0 3 3 = 4 - 8 3 = 4 3

Resposta

A = ∫ 0 2 2 y - y 2   d y = 4 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

92) Ache a área da região limitada pelo laço da curvas y 2 = x 2 . ( 4 - x ) .
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
90) Ache a área da região limitada pelas curvas y = s e n2 x e y = s e nx de x = 0 até x = π 3 .