Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 23
Use um recurso computacional para encontrar as aproximações pelas extremidades esquerda, direita e pelo ponto médio da área abaixo da curva acima do intervalo dado, usando subintervalos.
Passo 1
O exercício pede para utilizar um recurso computacional. Entretanto, podemos calcular também utilizando uma calculadora científica. Começando com a extremidade a esquerda. Determinaremos a área de cada segmento a esquerda e calcularemos o somatório de todos os pontos.
Se no intervalo
Significa que a cada passo acrescentamos de 1 até 2.
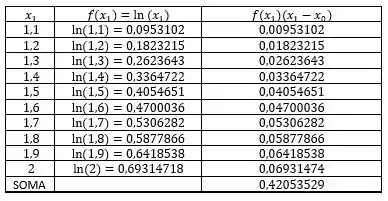
Vamos montar uma tabelinha bem bacana, onde calculamos todos os passos e o somatório total. Como se trata a esquerda calcularemos usando a fórmula:
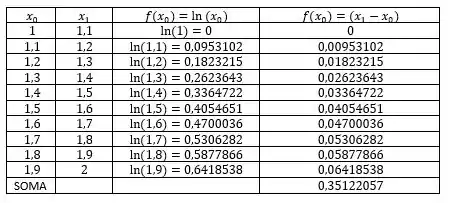
Passo 2
Como se trata do ponto médio calcularemos usando a fórmula:
Passo 3
Como se trata a direita calcularemos usando a fórmula:
