Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 37
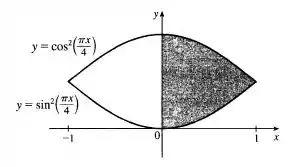
Use a Regra do Ponto Médio com para aproximar a área de uma região limitada pelas curvas dadas.
Passo 1
Pela regra do ponto médio, podemos escrever que
Onde é o valor da integral. Dessa forma, podemos definir nossa função
Precisamos também definir , que será
Passo 2
Encontrando o valor de , temos
Esboçando graficamente a função, temos
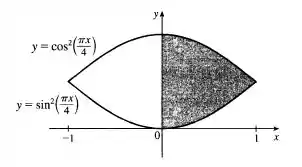
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada acima pela curva y = 1 / x 3 , abaixo pela curva - 1 / x 3 e a e
15- Determine o centro de massa de uma placa fina que abrange a região entre o eixo x e a curva y = 2 / x 2 , 1 ≤ x ≤ 2 , se a densidade da placa no ponto ( x , y ) for δ x = x 2 .
Determine as áreas das regiões compreendidas entre as retas e as curvas y = 2 x - x 2 E y = - 3
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 4 E y = 8 x
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 - 2 E y = 2