Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 50

Encontre o volume do sólido S descrito. Um tronco de pirâmide com base quadrada de lado b , topo quadrado de lado a e altura h .

O que acontece se a = b ? O que acontece se a = 0 ?

Passo 1

Fala aí! tudo certinho?

Nesse problema temos que encontre o volume do sólido S descrito como um tronco de pirâmide com base quadrada de lado b , topo quadrado de lado a e altura h .

Além disso queremos saber o que acontece se a = b e se a = 0 .

Podemos esboçar o seguinte desenho:

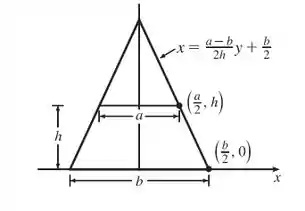
Veja só!

Passo 2

Uma das equações da reta é

x = ∆ x ∆ y y + i n t e r c e p t o - x = a 2 - b 2 h - 0 y + b 2 = a - b 2 h y + b 2

Encontrando o volume:

V = ∫ 0 h A y d y = ∫ 0 h 2 x 2 d y

V = ∫ 0 h 2 a - b 2 h y + b 2 2 d y

V = ∫ 0 h a - b h y + b 2 d y

V = ∫ 0 h a - b 2 h 2 y 2 + 2 b a - b h y + b 2 d y

Calculando a integral e aplicando os limites de integração...

V = a - b 2 3 h 2 y 3 + b a - b h y 2 + b 2 y 0 h

V = 1 3 a - b 2 h + b a - b h + b 2 h

Simplificando...

V = 1 3 a 2 - 2 a b + b 2 + 3 a b h

V = 1 3 a 2 + a b + b 2 h

Tranquilo até aqui?

Passo 3

Se a = b , nós temos um sólido retangular com volume

V = 1 3 b 2 + b b + b 2 h

V = b 2 h

Se a = 0 , temos uma pirâmide quadrada com volume

V = 1 3 0 2 + 0 + b 2 h

V = 1 3 b ² h

E aí! o que achou? Responde Aí!

Resposta

V = 1 3 a 2 + a b + b 2 h . Se a = b , nós temos um sólido retangular com volume b ² h . Se a = 0 , temos uma pirâmide quadrada com volume 1 3 b ² h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido S descrito. A base de S é a região elíptica limitada pela curva 9 x 2 + 4 y 2 = 36 . As secções transversais perpendiculares ao eixo x são triângulos isósceles retos com hi
Encontre o volume do sólido S descrito. S tem a mesma base do Exercício 58, mas as secções transversais perpendiculares ao eixo x são quadradas.
Encontre o volume do sólido S descrito. A base de S é a região triangular com vértices ( 0,0 ) ,( 1,0 ) , e ( 0,1 ) . As secções transversais perpendiculares ao eixo y são triângulos equiláteros.
A base de S é um disco circular com raio r . As secções transversais paralelas, perpendiculares à base, são triângulos isósceles de altura h e lado desigual na base. Estabeleça uma integral para o vol
Encontre o volume do sólido S descrito. S tem a mesma base do Exercício 60, mas as secções transversais perpendiculares ao eixo x são triângulos isósceles com altura igual à base.