Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 31
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.
31
Passo 1
O enunciado pede para gente calcular essa integral definida, usando as equações
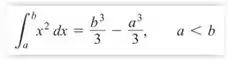
Passo 2
Vamos lá, para calcular essa integral usamos a primeira equação
Repara que nesse caso e
Então
Resposta
O resultado da integral é.
Exercícios de Livros Relacionados
Esboce o gráfico de cada função no intervalo dado. Em seguida, use fórmulas de área simples da Geometria para encontrar a função área A ( x ) que dá a área entre o gráfico da função f especificada e o
Esboce o gráfico de cada função no intervalo dado. Em seguida, use fórmulas de área simples da Geometria para encontrar a função área A ( x ) que dá a área entre o gráfico da função f especificada e o
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. Se a área sob a curva y = x 2 acima de um intervalo for aproximada pela área total de uma coleção de retângulos, então a apr
Repita o Exercício 23 para o intervalo [−3, 9].
Explique como usar a fórmula encontrada para A ( x ) na solução do Exemplo 2 para determinar a área entre o gráfico de y = x 2 e o intervalo [ 3 ,6 ] .