Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.5 - Ex. 2
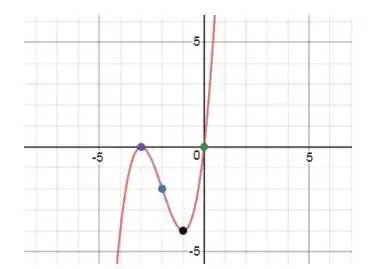
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema vamos usarmos o roteiro de esboço de curvas dado na seção para esboçar o gráfico da função dada por
Para iniciar a questão vamos relembrar um pouco da teoria:
Domínio: Conjunto de todos os valores de para os quais a função é definida.
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Simetria:
- Função Par:
- Função Ímpar:
Assíntotas:
- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.
- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Os intervalos nos quais uma função é crescente (ou decrescente) correspondem aos intervalos nos quais sua derivada é positiva (ou negativa). Então, se quisermos encontrar os intervalos em que uma função é crescente ou decrescente, nós calculamos sua derivada e descobrimos onde ela é positiva ou negativa (o que é mais fácil!).
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Bora lá!! 😉
Passo 2
Como se trata de um polinômio, o domínio é real:
Legal, né? 😁
Passo 3
Vamos achar as interseções com os eixos e . Para o ponto que corta o eixo , basta tomar , assim, . Vemos então que a curva passa pela origem . Para as interseções com o eixo , fazemos , assim
As raízes da função são e . Assim, as interseções com os eixos ocorrerão em e .
Note que tem expoentes pares e ímpares de , assim ela não é nem par nem ímpar. A função não tem nenhum tipo de simetria.
Tranquilo até aqui? 😊
Passo 4
Como se trata de um polinômio, não tem assíntotas:
Bora continuar! 😉
Passo 5
Para estudarmos os intervalos de crescimento e decrescimento, precisamos derivar :
*Para obtermos , basta resolver a equação . As raízes da equação são e , de modo que .
Desta forma,
Assim, é ponto de máximo local e é ponto de mínimo local. Note que e .
Mínimo local: ; máximo local: .
Interessante, né? 😇
Passo 6
Para a concavidade, precisamos da segunda derivada:
Assim,
Como , o ponto é um ponto de inflexão.
E finalmente, esboçando a curva, temos...
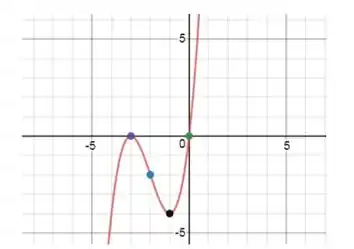
E aí! o que achou? Responde Aí! 👀
Resposta
Esboço da curva:
