Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 5

Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

∫ C y e x d x + 2 e x d y

C é um retângulo com os vértices 0,0 , 3,0 , 3,4   e   ( 0,4 ) .

Passo 1

E aí, gente!

Nessa questão precisamos calcular essa integral de linha aqui, ó:

∫ C y e x d x + 2 e x d y

Onde C é uma região retangular definido com vértices

0,0 , 3,0 , 3,4   e   ( 0,4 )

Podemos demonstrar essa região:

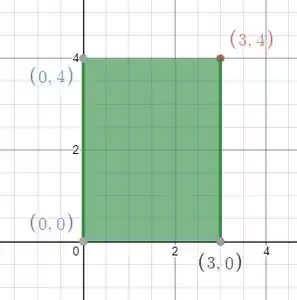
Como a questão pede, precisamos calcular com a fórmula do Teorema de Green. Essa aqui:

∬ P d x + Q d y = ∬ ∂ Q ∂ x - ∂ P ∂ y d A

Passo 2

Primeiro vamos encontrar nossos limites de integração.

No eixo x , temos que a região vai de

0 ≤ x ≤ 3

E no eixo y , temos

0 ≤ y ≤ 4

Belê. Agora precisamos descobrir quem são P e Q dados no enunciado, pra gente jogar na fórmula e fazer as derivadas parciais de primeira ordem.

∫ C y e x ⏟ P d x + 2 e x ⏟ Q d y

Jogando na fórmula, vamos ter

∬ ∂ Q ∂ x - ∂ P ∂ y d A

∬ ∂ ∂ x 2 e x - ∂ ∂ y y e x d A

E assim, com todas as informações...

∫ 0 4 ∫ 0 3 ( 2 e x - e x ) d x d y

Ou melhor...

∫ 0 4 ∫ 0 3 e x   d x   d y  

Passo 3

Agora vamos resolver nossa integral!

Começamos de dentro pra fora, ou seja, primeiro em relação a x !

∫ 0 3 ( e x ) d x

e x 0 3 = e 3 - e 0

Agora em relação a y :

∫ 0 4 e 3 - e 0 d y

Podemos colocar o que está em parênteses para fora da integral como uma constante, já que não temos nenhum termo com y :

( e 3 - 1 ) ∫ 0 4 d y

Integrando...

e 3 - 1 y 0 4 = 4 ( e 3 - 1 )

Show de bolinhaa!! 😊

Resposta

∮ C . y e x d x + 2 e x d y = 4 ( e 3 - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y 2 d x + x 2 y d y C é o retângulo com os vértices em 0,0 , 5,0 , 5,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x y d x + x 2 y 3 d y C é um triângulo com os vértices em 0,0 , 1,0e( 1,2 ) .