Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 3a

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

∮ C . x y d x + x 2 y 3 d y

C é um triângulo com os vértices em 0,0 , 1,0   e   ( 1,2 ) .

Passo 1

Fala, galera! Belezinha?? 😉

Nessa questão, precisamos calcular a integral de linha abaixo pelo método direto, segundo o que pede nosso item (a).

∮ C . x y d x + x 2 y 3 d y

Onde C é definido por um triângulo com os vértices em 0,0 , 1,0   e   ( 1,2 ) .

Que tal desenharmos a curva C primeiro de tudo?

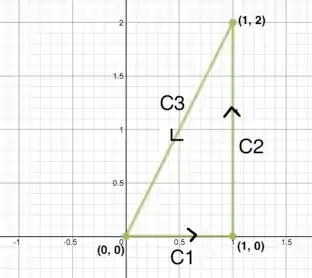
Para o nosso item (a), um jeito melhor de calcular essa integral de linha é quebrar ela em três integrais, uma pra cada trecho da curva representada acima. Assim,

∮ C . x y d x + x 2 y 3 d y = ∫ C 1 x y d x + x 2 y 3 d y + ∫ C 2 x y d x + x 2 y 3 d y + ∫ C 3 x y d x + x 2 y 3 d y

Passo 2

Precisamos, antes de tudo, encontrar os limites de integração C de cada integral acima. E por que existem três? Temos três caminhos, três retas...

Para o trecho C 1 , o valor de y é constante e igual a 0 , o que leva a d y = 0 . No caso de x , ele varia de 0 a 1 , mas ele é igual a zero. Por isso, podemos dizer que:

∮ C 1 . x y d x + x 2 y 3 d y = ∫ C 1 x 0 d x + x 2 0 3 0 = 0

Para o trecho C 2 , podemos observar que o valor de x é constante e igual a 1 , o que nos leva a ter d x = 0 .

∫ C 2 x y d x + x 2 y 3 d y

Substituindo...

∫ C 2 1 y 0 + 1 2 y 3 d y

No caso de y , temos uma variação ocorrendo de 0 a 2 (nosso novo limite de integração). Escrevendo a nossa integral, temos:

∫ 0 2 y 3 d y

y 4 4 0 2 = 16 4 = 4

Passo 3

Por fim, no trecho C 3 temos um segmento de reta indo do ponto ( 1,2 ) para o ponto ( 0,0 ) . A equação da reta, para esse caso é dada por:

y - y 0 = m ( x - x 0 )

Vamos calcular primeiro o coeficiente angular da reta m :

m = y - y 0 x - x 0 = 2 - 0 1 - 0 = 2

Logo, teremos:

y - 0 = 2 ( 1 - 0 )

y = 2 x       →     d y = 2 d x

Observe que estamos indo do ponto 1 a 0 , logo:

∫ C 3 x y d x + x 2 y 3 d y = ∫ 1 0 x 2 x d x + x 2 2 x 3 2 d x

∫ 1 0 2 x 2 d x + x 2 8 x 3 2 d x

Organizando...

∫ 1 0 2 x 2 + 16 x 5 d x

Calculando a integral e substituindo pelos limites de integração, teremos

2 x 3 3 + 16 x 6 6 1 0 = - 2 3 - 16 6 = - 10 3

Assim, como a integral de linha é a soma de todas as curvas C , isso é igual a:

∮ C . x y d x + x 2 y 3 d y = 0 + 4 - 10 3 = 2 3

Resposta

∮ C . x y d x + x 2 y 3 d y = 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7. ∮ C f → ⋅ d r → , onde f → = ( y , 0 ) e C é o triângulo de vértices A(0,1), B(3,1) e C(2,2), no sentido horário.
16. Dado o campo vetorial f → = y x 2 + y 2 , - x x 2 + y 2 , mostrar que ∮ C f → ⋅ d r → = - 2 π para toda curva fechada simples C, suave por partes, orientada no sentido anti-horário que circunda a
14. Determinar a área entre as elipses:(a) x^2 + 9 y^2 - 2 x - 18 y + 1 = 0 e x^2 - 2 x + 4 y^2 - 8 y + 4 = 0 .
Nos exercícios 1 a 11, calcular as integrais curvilíneas dadas usand o teorema de Green.1. ∮ C l n x - 2 y d x + 2 x + e y d y , ao longo da elipse x 2 + y 2 9 = 1 , no sentido horário.
Nos exercícios 1 a 11, calcular as integrais curvilíneas dadas usando o teorema de Green.6. ∮ C f → ⋅ d r → , onde f → = - 3 x 2 y , 3 x y 2 e C é a circunferência x 2 + y 2 + 4 y = 0 , no sentido ant