Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 1b

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

∮ C . y 2 d x + x 2 y d y

C é o retângulo com os vértices em 0,0 , 5,0 , 5,4   e   ( 0,4 ) .

Passo 1

Fala, pessoal! 😊

Nessa questão, precisamos calcular essa integral de linha aqui, ó:

∮ C . y 2 d x + x 2 y d y

Onde C é a região definida por um retângulo com vértices em

0,0 , 5,0 , 5,4   e   ( 0,4 )

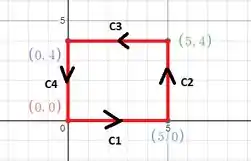
No nosso item (b) em específico, precisamos calcular através da fórmula do Teorema de Green, essa daqui:

∬ P d x + Q d y = ∬ ∂ Q ∂ x - ∂ P ∂ y d A

Onde precisamos fazer as derivadas parciais de P e Q e jogar na integral dupla, show?

Mas quem é cada um deles? Como iremos achar nossos limites de integração?

Vamos lá meter uma cotovelada na cara dessa questão!

Passo 2

Olhando para nosso gráfico acima, temos que no eixo x nossa região é calculável em:

0 ≤ x ≤ 5

E no eixo y a região é definida em

0 ≤ y ≤ 4

Beleza! Achamos nossos limites de integração para

d A = d x d y

Agora analisando a integral que nos foi dada pelo enunciado, vamos descobrir quem é P e Q :

∮ y 2 ⏟ P d x + x 2 y ⏟ Q d y

Usando o Teorema de Green, podemos escrever:

∬ ∂ Q ∂ x - ∂ P ∂ y d A

∬ ∂ ∂ x x 2 y - ∂ ∂ y y 2 d A

Fazendo as derivadas parciais de primeira ordem, ficaremos com:

∫ 0 4 ∫ 0 5 2 x y - 2 y d x d y

Passo 3

Agora vamos resolver nossa integral, primeiro em relação a x :

∫ 0 5 2 x y - 2 y d x

[ x 2 y - 2 x y ] 0 5

Substituindo pelos limites de integração, chegaremos a nossa próxima integral, agora em relação a y :

∫ 0 4 25 y - 10 y d y

Organizando...

∫ 0 4 15 y d y

Assim...

15 y 2 2 0 4 = 15 ⋅ 4 2 2 = 120

Show de bola!! 😉

Resposta

∮ C . y 2 d x + x 2 y d y = 120

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla. P x , y = 2 x - x 3 y 5 , Q x , y = x 3 y 8 C é uma elipse 4 x 2 +
Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla. P x , y = x 3 y 4 , Q x , y = x 5 y 4 C consiste de um segmento de
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C x y 2 d x + x 3 d y C é o retângulo com vértices 0,0 , 2,0 , 2,3 e 0,3 .