Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 4a

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

∮ C . x 2 y 2 d x + x y d y

C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o segmento de reta de ( 1,1 ) para ( 0,1 ) e de ( 0,1 ) para ( 0,0 ) .

Passo 1

Que tal desenharmos a curva C primeiro de tudo?!

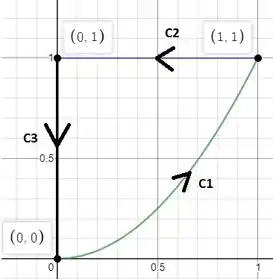
Um jeito melhor de calcular essa integral de linha é quebrar ela em três integrais, uma pra cada trecho da curva representada acima. Assim,

∮ C . x 2 y 2 d x + x y d y = ∫ C 1 x 2 y 2 d x + x y d y + ∫ C 2 x 2 y 2 d x + x y d y + ∫ C 3 x 2 y 2 d x + x y d y

Passo 2

Para o trecho C 1 , temos um arco de parábola com equação igual a y = x 2 . A derivada é igual a d y = 2 x d x . Assim, podemos escrever a integral

∫ C 1 x 2 y 2 d x + x y d y = ∫ 0 1 x 2 x 2 2 d x + x ( x 2 ) ( 2 x d x )

∫ C 1 x 2 y 2 d x + x y d y = ∫ 0 1 x 6 + 2 x 4 d x

∫ C 1 x 2 y 2 d x + x y d y = x 7 7 + 2 x 5 5 0 1

∫ C 1 x 2 y 2 d x + x y d y = 1 7 + 2 5 = 19 35

Passo 3

Para o trecho C 2 , podemos observar que o valor de y é constante e igual a 1 , o que nos leva a ter d y = 0 . No caso de x , temos uma variação ocorrendo de 1 a 0. Escrevendo a nossa integral, temos:

∫ C 2 x 2 y 2 d x + x y d y = ∫ C 2 x 2 1 2 d x + x ( 1 ) ( 0 )

∫ C 2 x 2 y 2 d x + x y d y = ∫ 1 0 x 2 d x

∫ C 2 x 2 y 2 d x + x y d y = x 3 3 1 0

∫ C 2 x 2 y 2 d x + x y d y = - 1 3

Passo 4

Por fim, no trecho C 3 temos y variando de 1 para 0 . Além disso, o valor de x é constante e igual a zero, levando a ter d x = 0 . Assim, temos:

∫ C 3 x 2 y 2 d x + x y d y = ∫ C 3 0 2 y 2 ( 0 ) + ( 0 ) y d y

∫ C 3 x 2 y 2 d x + x y d y = 0

Assim, a integral de linha é igual a:

∮ C . x 2 y 2 d x + x y d y = 19 35 - 1 3 + 0 = 22 105

Resposta

A integral de linha é igual a:

∫ C x 2 y 2 d x + x y d y = 22 105

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y 2 d x + x 2 y d y C é o retângulo com os vértices em 0,0 , 5,0 , 5,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y d x - x d y C é uma circunferência com centro na origem e r a i o = 4 .
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C x 2 + y 2 d x + x 2 - y 2 d y C é um triângulo com os vértices 0,0 , 2 , 1e0 , 1 .
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y 4 d x + 2 x y 3 d y C é a elipse x 2 + 2 y 2 = 2 .
Uma partícula começa na origem, se move ao longo do eixo x para o ponto ( 5,0 ) , em seguida ao longo do quarto da circunferência x 2 + y 2 = 25 ,x ≥ 0 ,y ≥ 0 para o ponto ( 0,5 ) , e então para baixo