Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 1a

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

∮ C . y 2 d x + x 2 y d y

C é o retângulo com os vértices em 0,0 , 5,0 , 5,4   e   ( 0,4 ) .

Passo 1

E aí, pessoal! Tranquilo?

Nossa questão quer que a gente calcule a integral:

∮ C . y 2 d x + x 2 y d y

Diretamente. A região C onde estamos integrando é: o retângulo com os vértices em 0,0 , 5,0 , 5,4   e   ( 0,4 ) . Traçando os pontos do retângulo, temos:

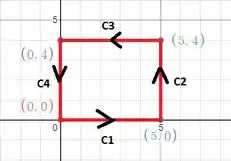
Uma boa abordagem pra resolver essa questão é dividir a integral em 4 partes mais simples! Assim,

∮ C . y 2 d x + x 2 y d y = ∮ C 1 + C 2 + C 3 + C 4 y 2 d x + x 2 y d y

Ou seja, vamos calcular nossa integral 4 vezes, cada vez com os limites de integração correspondendo a um trecho de C e no final, somamos os 4 resultados para obtermos o valor da nossa integral sobre a região completa.

Vamo lá!

Passo 2

Retomando a imagem da nossa região C :

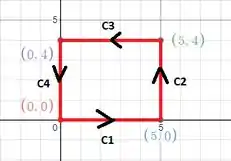
Para o primeiro trecho C 1 , não há variação no valor de y pois ele é constante, logo y = 0 e d y = 0 .

∮ C 1 . y 2 d x + x 2 y d y = ∮ C 1 0 2 d x + x 2 ( 0 ) ( 0 )

Então, nossa integral será:

∮ C 1 . y 2 d x + x 2 y d y = 0

Passo 3

Para o segundo trecho C 2 , podemos observar que o valor de x é constante, levando a ter d x = 0 . Já no caso de y , nós temos uma variação de 0 a 4 . Assim,

∮ C 2 . y 2 d x + x 2 y d y = ∮ C 2 y 2 0 + 5 2 y d y

Ficamos somente com o termo:

∮ C 2 y 2 0 + 5 2 y d y = ∫ 0 4 25 y d y

Integrando:

∫ 0 4 25 y d y = 25 y 2 2 0 4

Agora basta aplicarmos nossos limites de integração:

∫ 0 4 25 y d y = 25 × 4 2 2 - 25 × 0 2 2 = 200

Então:

∮ C 2 . y 2 d x + x 2 y d y = 200

Passo 4

Já o trecho C 3 nos mostra que o valor de y é constante e igual a 4 , levando a ter d y = 0 . No caso de x , temos uma variação de 5 para 0 . Assim,

∮ C 3 . y 2 d x + x 2 y d y = ∮ C 3 4 2 d x + x 2 ( 4 ) ( 0 )

Ficamos somente com a integral de um termo:

∮ C 3 4 2 d x + x 2 ( 4 ) ( 0 ) = ∫ 5 0 16 d x

Integrando e aplicando os limites de integração:

∫ 5 0 16 d x = 16 0 - 5 = - 80

Então:

∮ C 3 . y 2 d x + x 2 y d y = - 80

Passo 5

Por último, o trecho C 4 nos mostra que o valor de x é constante, levando a ter d x = 0 . Nesse caso, o valor de y nós temos uma variação de 4 para 0 . Assim,

∮ C 4 . y 2 d x + x 2 y d y = ∮ C 3 y 2 ( 0 ) + 0 2 y d y

Então:

∮ C 4 . y 2 d x + x 2 y d y = 0

Assim, o valor total da integral é igual a:

∮ C . y 2 d x + x 2 y d y = 0 + 200 - 80 + 0 = 120

Resposta

A integral de linha é igual a:

∮ C . y 2 d x + x 2 y d y = 120

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. Determinar a área entre as elipses:(a) 4 x^2 + y^2 = 4 e (x^2)/(9) + (y^2)/(4) = 1
Sejam B e gamma como no Exercício 10. Prove queÁrea de B = - int_gamma y d x
Sejam f ,g : a , b → R duas funções de classe C 1 tais que, para todo x em a , b , f xg x . Seja B o conjunto de todos x , y tais que f x ≤ y ≤ g x , a ≤ x ≤ b . Seja γ a fronteira de B orientada no s
Verifique a relação do exercício anterior supondo B o quadrado de vértices - 1 , - 1 , 1 , - 1 , 1,1 e - 1,1 ; γ a fronteira de B orientada no sentido anti-horário.
Verifique que ∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x d y Onde B é o triângulo de vértices 0,0 , 1,0 e 1,1 ; γ é a fronteira de B orientada no sentido anti-horário, P x , y = x 2 - y e Q x , y =