Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.4 - Ex. 13

Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.)

F x , y = x + y 3 , x 2 + y

C consiste no arco da curva y = sen ⁡ x de ( 0,0 ) a ( 0 , π ) e no segmento de reta ( π , 0 ) a ( 0,0 )

Passo 1

Temos C como a seguinte curva no plano

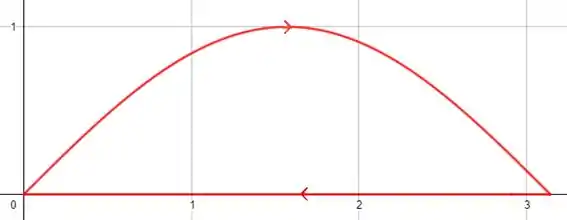
Da maneira que está descrita a curva temos uma orientação negativa, então para aplicar o teorema, precisaremos usar na integral sobre - C , pela relação

∫ C F ⋅ d r = - ∫ - C F ⋅ d r

Onde a segunda integral tem orientação positiva e podemos aplicar o Teorema de Green.

Passo 2

Aplicando o teorema na segunda integral

∫ - C x + y 3 , x 2 + y ⋅ d r = ∬ D ∂ ∂ x x 2 + y - ∂ ∂ y x + y 3 d A

= ∬ D 2 x - 3 y 2   d A = ∫ 0 π ∫ 0 sen ⁡ x 2 x - 3 y 2   d y d x

= ∫ 0 π 2 x y - y 3 0 sen ⁡ x d x = ∫ 0 π 2 x sen ⁡ x - sen 3 ⁡ x d x

Passo 3

Para o primeiro termo da integral vamos calcular por partes

∫ 2 x sen ⁡ x d x

Seja

f = 2 x   → f ' = 2

g ' = sen ⁡ x   → g = - cos ⁡ x

Temos que

∫ 2 x sen ⁡ x d x = - 2 x cos ⁡ x + 2 ∫ cos ⁡ x d x

∫ 2 x sen ⁡ x d x = - 2 x cos ⁡ x + 2 sen ⁡ x + C

Para o segundo termo temos

∫ sen 3 ⁡ x = ∫ sen 2 ⁡ x sen ⁡ x d x = ∫ 1 - cos 2 ⁡ x sen ⁡ x d x

Substituindo

u = cos ⁡ x

d u = - sen ⁡ x d x

∫ 1 - cos 2 ⁡ x sen ⁡ x d x = ∫ 1 - u 2 ( - d u )

= ∫ ( u 2 - 1 ) d u = u 3 3 - u + C

Substituindo de volta

∫ sen 3 ⁡ x = cos 3 ⁡ x 3 - cos ⁡ x + C

Passo 4

Voltando a integral definida

∫ 0 π 2 x sen ⁡ x - sen 3 ⁡ x d x = - 2 x cos ⁡ x + 2 sen ⁡ x + cos ⁡ x - cos 3 ⁡ x 3 0 π

= - 2 π cos ⁡ π + 2 sen ⁡ π + cos ⁡ π - cos 3 ⁡ π 3 - 1 - 1 3

= - 2 π ( - 1 ) + 2 ( 0 ) + ( - 1 ) - - 1 3 3 - 2 3

= 2 π - 1 + 1 3 - 2 3 = 2 π - 4 3

Como temos

∫ C F ⋅ d r = - ∫ - C F ⋅ d r

∫ C F ⋅ d r = - 2 π - 4 3

∫ C F ⋅ d r = 4 3 - 2 π

Resposta

∫ C F ⋅ d r = 4 3 - 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

f ( x , y ) = x 3 / y ,C : y = x 2 / 2 ,0 ≤ x ≤ 2
f ( x , y ) = x + y 2 / 1 + x 2 , C : y = x 2 / 2 entre ( 1,1 / 2 ) e ( 0,0 )