Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.4 - Ex. 14
Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)
é o triangulo de a a a
Passo 1
Olá, tudo bem? Vamos ver o que a questão quer.
Ela quer que a gente calcule a integral de linha
onde é a linha de um triângulo que está localizado nos pontos de a a a
E é
Utilizando o Teorema de Green
Que diz que podemos transformar uma integral de linha em uma integral dupla utilizando a relação acima.
Onde, na integral de linha é tudo que está na coordenada do vetor
e é tudo que está na coordenada do vetor
e é o contorno da curva que nesse caso é o triângulo!
E na integral dupla que vamos fazer, é o interior da curva que precisa estar orientada positivamente que nessa questão é a área do triângulo!
É a derivada parcial de em relação à ,
É a derivada parcial de em relação à e
Por que usar o Teorema de Green?
Primeiro porque que a questão pede pra fazer isso 🤣 e segundo porque facilita muito os cálculos!
Portanto,
Primeiro, identificaremos e e calcularemos suas derivas parciais, depois montaremos a integral com elas, analisaremos a região e calcularemos a integral.
Partiu?
Passo 2
Nosso primeiro passo é obter e . A integral de linha é:
Onde
Sendo tudo que está localizado na coordenada do vetor
e tudo que acompanha , temos
Calculando em relação à :
Calculando em relação à :
Portanto,
Passo 3
Agora montaremos a integral. Temos
Substituindo o que achamos no passo anterior:
E lembrando que
Então,
Passo 4
Vamos analisar a nossa região !
Primeiro vamos olhar como a seguinte curva no plano
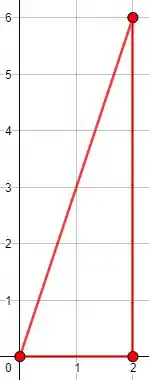
Da maneira que está descrita a curva temos uma orientação negativa, pois está de , depois , depois e por último que é o sentido horário!
Ou você pode pensar que enquanto anda pela linha do triângulo, o interior dele precisar estar na esquerda para estar orientada positivamente!
Então para aplicar o teorema, precisaremos usar a integral sobre , temos a relação
Onde a segunda integral tem orientação positiva, e aplicando no Teorema de Green:
Simplesmente colocamos um sinal negativo na integral do Teorema de Green, pois a curva está orientada negativamente, ok?
Vamos então, achar os limites da região :
Temos na figura
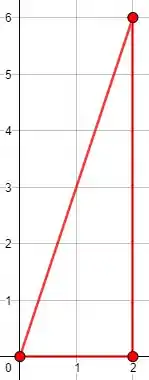
variando de à
E variando de à reta inclinada,
Que podemos descobrir sua função, primeiro fazendo a diferença entre e de dois pontos dela e para descobrir o coeficiente angular:
Sendo o coeficiente angular :
E como a reta passa pela origem, . Então:
Portanto
Passo 5
Colocando os limites e resolvendo a integral:
Sempre lembrando que o limite de integração com mais variáveis fica no interior!
Resolvendo em relação à :
Resolvendo em relação à :
Prontinho!