Exercícios de Teorema de Green para Curvas Abertas - Lista de Exercícios Resolvida
Questão 1
Calcular a integral de linha da função vetorial
Ao longo da curva que liga o ponto ao ponto e é definida pela equação .
Ver solução completaQuestão 2
Calcule , onde é o arco da circunferência , no primeiro quadrante, orientado no sentido anti-horário.
Ver solução completaQuestão 5
Calcule , onde é a parte da curva contida no semiplano orientada no sentido anti-horário.
Ver solução completaQuestão 8
Calcule , onde é a parte da curva contida no semiplano orientada no sentido anti-horário.
Ver solução completaQuestão 9
17) Calcule as seguintes integrais:
a)
Onde é formada por e , , que vai do ponto ao ponto .
Ver solução completaQuestão 10
Seja uma curva simples por partes, contida no conjunto aberto:
Com exceção no ponto inicial e do ponto final . Supondo que a área limitada pela curva e pelo eixo cartesiano é dada por , calcule:
Ver solução completaQuestão 12
Questão 3:
Seja o campo vetorial plano
e seja o caminho orientado dado pela concatenação das curvas regulares orientadas , e , onde é o segmento que parte do ponto e vai até , é o arco da curva , partindo de até o segmento que parte de até .
Calcule .
Dica: Feche o caminho com um arco da curva indo de até para obter um caminho simples.
Ver solução completaQuestão 13
Usando o Teorema de Green, calcular
Onde é o campo vetorial e é a curva por partes formada por e , , que vai do ponto ao ponto .
Ver solução completaQuestão 14
18) Calcule o trabalho realizado pelo campo de forças
ao mover uma partícula ao longo da trajetória dada por .
Ver solução completaQuestão 16
Seja uma curva simétrica em relação ao eixo , que vai de a , como mostrada na figura abaixo. Sabendo-se que a área da região delimitada por e o eixo vale 16, calcule o trabalho realizado pela força
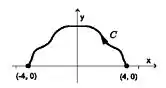
Questão 17
Seja uma curva orientada, composta dos segmentos de reta que ligam os pontos a , a , a , onde e são números reais positivos. Mostre que:
Para qualquer função de classe definida em todo .
Ver solução completaQuestão 20
Considere o campo vetorial no plano dado por
Calcule a integral de linha , onde é a parte da elipse contida no primeiro quadrante, com ponto inicial e ponto final .
Ver solução completaQuestão 21
Questão 3: Seja
Calcule , onde é o semicírculo dado por , , e percorrido de até .
Ver solução completaQuestão 22
Calcule a integral de linha , onde é o arco de elipse com , orientada de a .
Ver solução completaQuestão 23
17) Calcule as seguintes integrais:
b)
Onde é a curva , , percorrida de a .
Ver solução completaQuestão 24
17) Calcule as seguintes integrais:
d)
Onde é o arco de parábola , orientado de a .
Ver solução completaQuestão 25
17) Calcule as seguintes integrais:
c)
Onde é a poligonal aberta que une os pontos , e , nesta ordem.
Ver solução completaQuestão 26
4) Seja o hemisfério superior da circunferência , percorrida com ponto inicial e ponto final . O valor da integral de linha é:
Questão 27
Seja a curva em parametrizada por
Calcule a área que fica entre a curva e o eixo .
Sugestão: aplicar o Teorema de Green, usando um campo vetorial tal que
Ver solução completaQuestão 28
Questão 2: Utilize o Teorema de Green para calcular a integral de linha
Onde é o pedaço do gráfico com ponto inicial e ponto final .
Lembrete:
Ver solução completaQuestão 29
Questão 3: Considere o campo e a curva regular por partes onde:
- é o segmento de reta do ponto até o ponto .
- é o arco da parábola de equação do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
- é o arco da parábola de equação do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
Calcule
Dica: Para aplicar o teorema de Green é necessário fechar a curva. Para facilitar partes das integrais, use a curva que faz com que a região limitada por sua fronteira seja simétrica em relação ao eixo e ao eixo .
Passo 1
Primeiro, para entendermos o problema, acho útil desenharmos a curva:
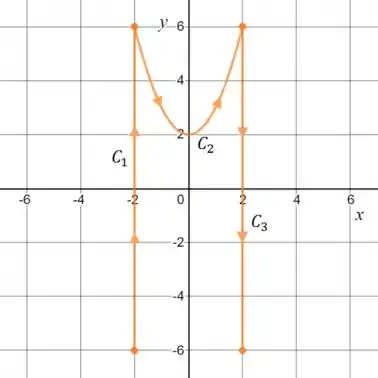
Perceba que a curva é uma composição bem louca, logo, para calcular a integral de linha seria interessante pensarmos no Teorema de Green:
Ver solução completaQuestão 30
Sejam o campo vetorial plano definido por e a curva regular dada pela equação e a desigualdade
Orientada indo do ponto ao ponto
a) Esboce
b) Determine uma parametrização da curva regular que é o segmento de reta que liga os pontos e .
c) Use o teorema de Green para calcular a integral
(Dica: Use a concatenação de do item (b), para obter a curva fechada simples.)
Ver solução completaQuestão 31
Sejam os campos vetoriais definidos como:
Calcule
Sendo o arco da circunferência de raio , que liga a com
Ver solução completaQuestão 32
Questão 2: Calcule a integral de linha
Onde é o trecho da curva , do ponto ao ponto .
Ver solução completaQuestão 33
Calcule a integral de linha do campo vetorial
sobre a curva parametrizada por , onde .
Ver solução completaQuestão 34
Seja o trecho da elipse com , de (2,0) a (0,0). A integral é igual a:
Ver solução completaQuestão 36
Calcule para a curva dada por com percorrida no sentido anti-horário.
Ver solução completaQuestão 38
Calcular a integral de linha da função vetorial
Ao longo da curva que liga o ponto ao ponto e é definida pela equação .
Ver solução completaQuestão 40
Questão um: utilizando o teorema de Green, calcular o valor da integral de linha do campo vetorial sobre o contorno aberto , definido na Fig. , com ponto inicial e ponto final .
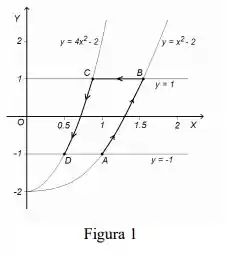
Questão 41
Questão 3: Seja o campo
E o arco da curva de até . Usando o Teorema de Green calcular
Ver solução completa
