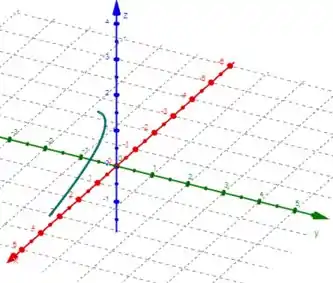
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Passo 1
Eaee, belezinha?? Bom... O enunciado nos deu a seguinte função vetorial:
Queremos plotar a sua curva e, para isso, precisaremos utilizar um software matemático.
Além disso, queremos escolher bem o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Agora bora lá!! 😉
Passo 2
Essa curva esta parametrizada pelo parâmetro , para traçar ela precisamos escolher um domínio para esse parâmetro e aqui podemos escolher todos os números reais que não terá nenhum problema, devido ao fato de suas componentes serem contínuas, portanto:
Para termos uma visualização real da curva parametrizada dada, é necessário uma visão ampla, abrangendo os 3 planos coordenados simultaneamente, veja:
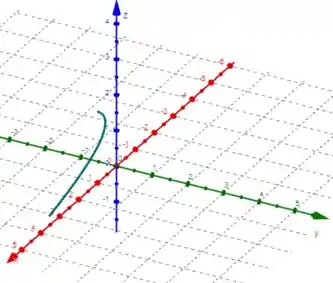
Esse é o melhor ângulo que podemos enxergar a figura 😉.
Aah... só lembrando que ela está no lado positivo de cada uma das coordenadas (perceba que faz sentido porque em cada uma das equações paramétricas só resultam em valores positivos para valores de onde a função existe).
Veja outras perspectivas dela ao rotacionar o eixo no sentido horário:
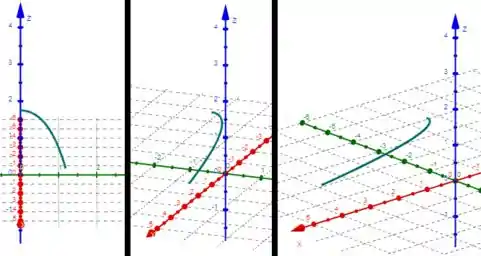
Resposta