Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 30

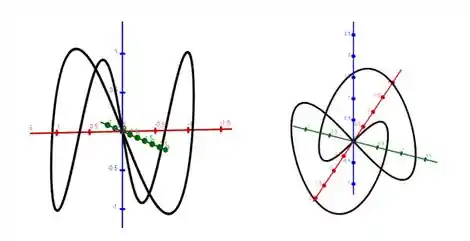
Utilize o computador para traçar a curva da equação vetorial dada. Escolha o dom��nio do parâmetro e ponto de vista de forma a garantir que a visualização é verdadeira.

Passo 1

Eaee, belezinha?? Bom... O enunciado nos deu a seguinte função vetorial:

Queremos plotar a sua curva e, para isso, precisaremos utilizar um software matemático.

Além disso, queremos escolher bem o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.

A partir das equações paramétricas, e analisando suas interseções com os planos coordenados podemos descobrir a forma da curva.

As equações paramétricas são:

Agora bora lá!! 😉

Passo 2

Teremos senos de diferentes frequências, porém de mesma amplitude em cada par de eixos.

Para uma visualização completa dessa curva, é necessário dois pontos de vista diferentes, onde o parâmetro assume valores entre

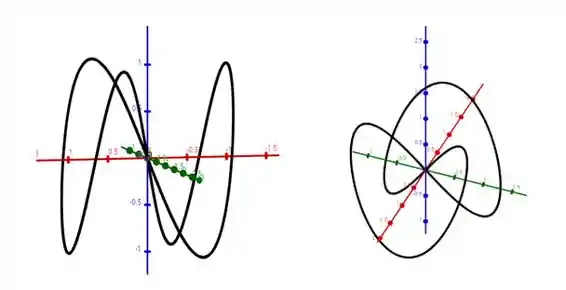
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas: x = t , y = 1 ( 1 + t 2 ) , z = t 2

Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas: x = t cos ⁡ t , y = t , z = t sin ⁡ t , t ≥ 0

Combine as equações paramétricas com os gráficos (rótulo I-VI). Dê razões para suas escolhas: x = cos ⁡ t , y = sin ⁡ t , z = cos ⁡ 2 t

Esboce a curva com a equação vetorial fornecida. Indique uma seta, o sentido na qual t aumenta: r t = 2 cos ⁡ ti → + 2 sin ⁡ tj → +k →

Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas: x = cos 2 ⁡ t , y = sin 2 ⁡ t , z = t