Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 21
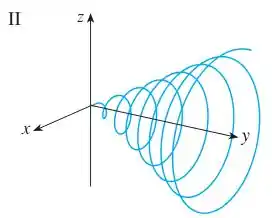
Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas:
, , ,
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu as seguintes equações paramétricas:
, ,
Para .
Queremos saber qual das figuras abaixo essa equação se encaixa:
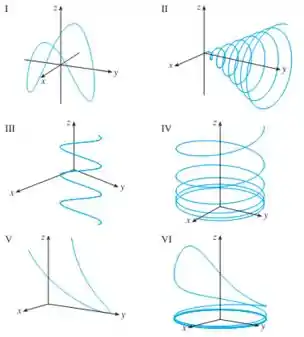
Para descobrirmos isso, temos que analisar cada uma das três equações paramétricas dadas e fazer relações entre elas.
Mas como assim??
Podemos fazer relações de como elas se comportam no plano bidimensional analisando apenas duas delas.
Em seguida, aplicarmos a terceira equação para vermos o comportamento no plano tridimensional.
Quer saber como?? Bora junto!!
Passo 2
Bom galera, a gente lembra que a equação paramétrica do circulo é:
E o do problema é:
Hmmmmm.. reparou???
Se analisarmos apenas e , teremos um circunferência em que seu raio cresce à medida que aumenta.
Assim, analisando apenas o plano bidimensional e , teríamos uma espiral!!
Agora vamos analisar !
Passo 3
Analisando , temos:
Perceba que quando aumentamos , também aumenta!!
Assim, a nossa espiral se torna um “furação” com centro em !!
A gente pode perceber isso na Figura 2:
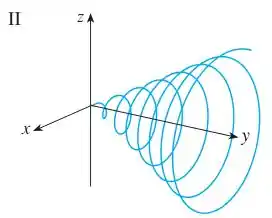
Resposta
