Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 12
Esboce a curva com a equação vetorial fornecida. Indique uma seta, o sentido na qual aumenta:
Passo 1
Eaee, belezinha?? Bom... O enunciado nos deu a seguinte equação vetorial:
Queremos esboçar essa equação e mostrar o sentido na qual aumenta.
Para isso, podemos imaginar que estamos fazendo uma parametrização de curvas onde, de acordo com a equação, podemos dizer que:
Perceba que , ou seja, basta analisarmos e sabendo que essa nossa figura (bidimensional por estarmos tratando apenas de e ) estará no plano em que .
Em seguida, podemos atribuir valores de e analisar como está o crescimento de , e .
Passo 2
Bom galera, como a gente pode ver, mesmo sendo trididimensional o a linha encontra-se apenas em .
Agora, vamos analisar as duas equações que restaram:
Pera... se a gente analisar bem, percebemos que trata-se de uma circunferência de raio centrada na origem!!
Passo 3
Agora vamos calcular alguns pontos para analisarmos o crescimento de :
Para , temos:
Para , temos:
Para , temos:
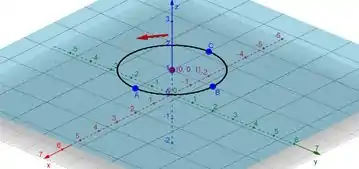
Então a gente sabe que é um circulo que irá passar por esses pontos e apenas no , o gráfico fica:
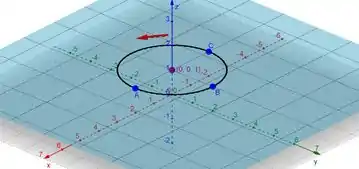
E a seta aponta a o sentido da curva.
Resposta
