Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.2 - Ex. 4
Utilize uma tabela de valores numéricos de para perto da origem para conjecturar sobre o limite de quando . Em seguida, explique por que sua conjectura está correta.
Passo 1
Pessoal, primeiro vamos fazer uma tabela com os valores de para vários valores de perto da origem:
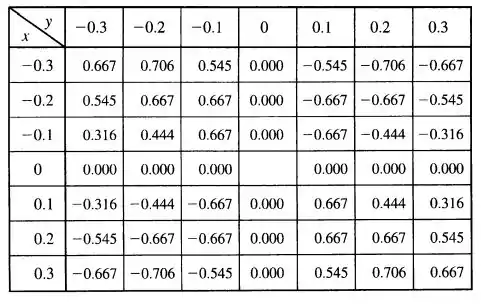
Como a tabela mostra, os valores de não parecem se aproximar de um único valor. Então vamos conjecturar que o limite não existe.
Passo 2
Show! Agora vamos tentar provar que nossa conjectura é verdadeira. Pra provar que o limite não existe, temos que encontrar valores diferentes de limites quando nos aproximarmos da origem por curvas diferentes.
Primeiro, vamos nos aproximar de ao longo do eixo , ou seja, fazendo :
E agora, ao longo da reta :
Realmente, o limite não existe!
Resposta
O limite não existe.