Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 81
(a) Mostre que, tomando logaritmos, a função geral de Cobb-Douglas pode ser expressa como
(b) Se tomarmos e , a equação da parte (a) se tornará uma equação linear . Utilize a Tabela 2 (do Exemplo 3) para fazer uma tabela de valores de e para os anos de 1899-1922. Use então um computador ou calculadora gráfica para achar, pelo método dos mínimos quadrados, a reta de regressão pelos pontos .
(c) Deduza que a função de produção de Cobb-Douglas é .
Passo 1
Olá, meu amigo. Tudo bem? Vamos resolver juntos essa atividade. Ela é um pouco grande, mas vamos em partes.
Primeira coisa que ela nos pede é para reescrevermos a função:
Utilizando logaritmos. Para isso, vamos lembrar de algumas propriedades de logaritmos, que iremos utilizar para provar o que eles pedem.
A primeira é:
E a segunda:
Agora vamos para mais uma propriedade:
Com essas propriedades a gente consegue resolver o que nos pediram.
A segunda parte envolve muitas coisas ao mesmo tempo heheh. Primeiro deveremos chamar de:
E
Teremos que a equação da letra a) que provamos se tornará uma equação linear de equação:
Deveremos então utilizar da tabela 2,
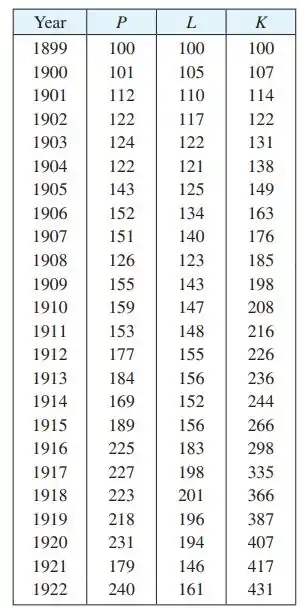
e encontrarmos dados entre os anos , após isso, iremos utilizar um software gráfico para gerar a reta a partir dos dados da tabela gerada.
Por último, mas não menos importante, iremos deduzir que
Faremos isso comparando a equação que iremos encontrar com o software com a equação:
Passo 2
(a) Galera, vamos partir da equação que define a função de Cobb-Douglas e tomar o logaritmo de ambos os lados:
Aplicando o logaritmo neperiano em ambos os lados:
Utilizando a propriedade de produto para soma:
Agora vamos utilizar a propriedade do valor elevado:
Agora iremos reorganizar a equação:
E agora por último iremos utilizar a propriedade da subtração para divisão:
Passo 3
(b) Agora vamos fazer uma tabela de valores de e para os anos de 1899-1922:
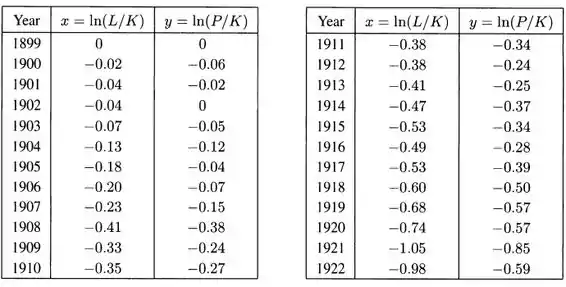
Fazendo uma regressão linear por meio do Excel, obtemos a seguinte reta:
Para obtermos essa reta por meio do Excel deveremos reescrever essa tabela nele, selecionarmos os dados, e pedirmos para inserir um gráfico. No gráfico, iremos adicionar a equação da reta.
Vamos arredondar assim:
Passo 4
(c) Se compararmos a equação da reta obtida no passo anterior por regressão linear com , descobrimos que:
Então, substituindo os valores encontrados de cada parâmetro da função de produção de Cobb-Douglas, obtemos:
Resposta
(b)