Para quais valores de a integral converge? Qual é o valor da integral quando ela converge ? Trace o gráfico do integrando para vários valores de
Passo 1
Incialmente analisaremos a integral impropria. Para isso é importante lembrar que
Ou seja, precisamos avaliar quando e quando . Sendo assim, separaremos nosso intervalo de integração em dois, ou seja,
Passo 2
Analisando,
Veremos que
Para calcularmos as integrais improprias acima, precisaremos chamar , para assim tomarmos o limite de e chamaremos , para assim tomarmos o limite de . Sendo assim,
Utilizando integração por partes, suponha
,
Sendo assim,
Logo,
De maneira análoga encontraremos que
Passo 3
Perceba que,
Precisamos agora, analisar os valores que deve assumir, para que a integral seja convergente.
Analisando o limite que está dando problema teremos
Perceba que quando teremos que o limite será da forma:
Reescrevendo a função,
Sendo assim podemos utilizar L’Hospital, ou seja,
Daí,
Logo,
Portanto, é convergente para
Passo 4
Perceba que,
Desejamos encontrar um valor de , de maneira que exista. Sendo assim, perceberemos que para , teremos,
Isso acontece, pois como então a potência vai para o denominador com o expoente positivo.
Chegamos numa indeterminação do tipo . Com isso, podemos utilizar L’Hospital, ou seja,
Já quando olhamos para o outro limite e supomos que obtemos também que
Portanto,
Portanto,
Converge para e quando isso acontece,
Passo 5
Perceba que na integral que queremos analisar,
precisamos estabelecer quais valores fazem com que aquelas duas integrais sejam convergentes simultaneamente. Porém, ao analisarmos cada uma vimos que para o intervalo de , já no intervalo , isso significa que não como estabelecermos valores para de maneira que as duas integrais sejam convergentes ao mesmo tempo.
Logo,
Diverge independentemente do valor que assumir.
Passo 6
Relembrando o exercício 80, saberemos que
Diverge independentemente do valor que assumir.
Como,
E ambas as integrais divergem independentemente do valor que assumir.
Portanto,
Diverge independentemente do valor que assumir.
Plotando o gráfico de ,
Para
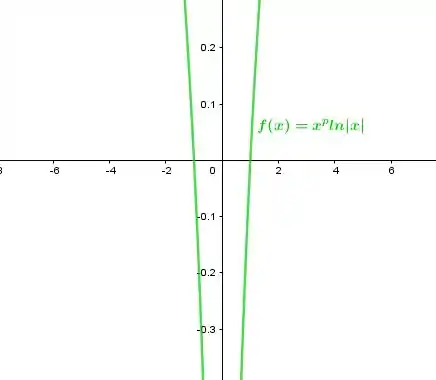
Para
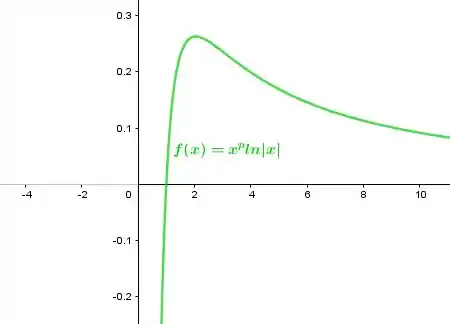
Para
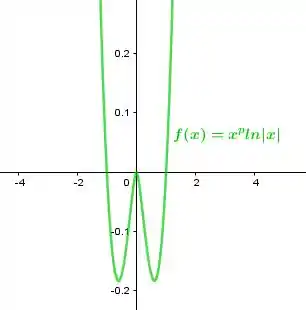
Para
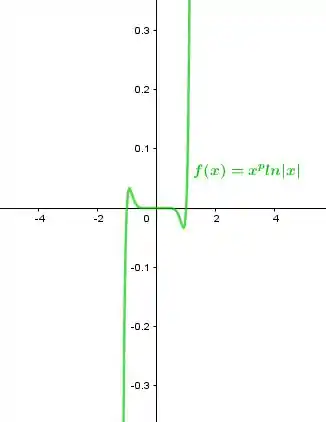
Resposta
Diverge independentemente do valor que assumir.