Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 11.4 - Ex. 24

Nos exercícios de 1 a 25, determine se a integral imprópria é convergente ou divergente. Se for convergente , calcule-a.

24. ∫ 0 1 d x x 4 - x 2  

Passo 1

Beleza galera, pra começar, o enunciado já diz que a integral é imprópria. Sendo assim, ou alguma limite de integração é infinito, o que não é nosso caso, ou existe uma descontinuidade em algum x tal que:

0 ≤ x ≤ 1

Nesse caso, exatamente em x = 0 temos uma descontinuidade, afinal:

1 x 4 - x 2   x = 0 = 1 0 =         ? ? ? ? ? ?

Portanto a forma certa de resolver essa integral é modificando ela da seguinte forma:

∫ 0 1 d x x 4 - x 2   = lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2  

Nossos passos serão:

  1. Resolver a integral de forma indefinida
  2. Aplicar os limites de integração de a até 1
  3. Aplicar o limite a → 0 +

Passo 2

Show, vamos pro nosso primeiro passo, calcular:

∫ d x x 4 - x 2  

Essa integral tem uma super cara de que sai por substituição trigonométrica. Checa só a tabela:

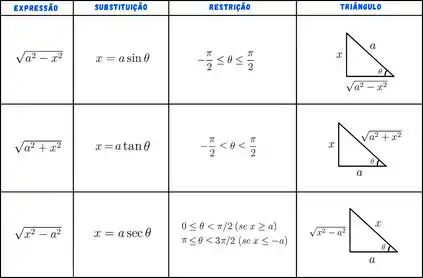
No nosso caso, temos exatamente a primeira linha, com a 2 = 4 e logo a = 2 . Portanto a substituição que faremos será:

x = 2 sen ⁡ θ

d x = 2 cos ⁡ θ   d θ

Pelo triângulo auxiliar ainda, tiramos que:

cos ⁡ θ = a 2 - x 2 a

a 2 - x 2 = a   cos ⁡ θ

O que no nosso caso é o mesmo que:

4 - x 2 = 2   cos ⁡ θ

Realizando essas substituições:

∫ d x x 4 - x 2   = ∫ 2 ∙ cos ⁡ θ   d θ 2 ∙ sen ⁡ θ ∙ 2 ∙ cos ⁡ θ   = 1 2 ∫ d θ sen ⁡ θ   = 1 2 ∫ csc ⁡ θ d θ

E opa, a integral que sobrou é uma de resolução direta, vamos ter:

∫ d x x 4 - x 2   = 1 2 - ln ⁡ csc ⁡ θ + ctg ⁡ θ

∫ d x x 4 - x 2   = 1 2 - ln ⁡ 1 sen ⁡ θ + cos ⁡ θ sen ⁡ θ

∫ d x x 4 - x 2   = - 1 2 ln ⁡ 1 + cos ⁡ θ sen ⁡ θ

Pelo triângulo auxiliar, tiramos:

cos ⁡ θ = 4 - x 2 2

sen ⁡ θ = x 2

E logo:

∫ d x x 4 - x 2   = - 1 2 ln ⁡ 1 + 4 - x 2 2 x 2 = - 1 2 ln ⁡ 2 + 4 - x 2 x

Passo 3

Bora agora aplicar os limites de integração! Vamos ter:

∫ 0 1 d x x 4 - x 2   = - 1 2 ln ⁡ 2 + 4 - x 2 x x = a x = 1

∫ 0 1 d x x 4 - x 2   = - 1 2 ln ⁡ 2 + 4 - 1 1 - - 1 2 ln ⁡ 2 + 4 - a 2 a

∫ 0 1 d x x 4 - x 2   = - 1 2 ln ⁡ 2 + 3 + 1 2 ln ⁡ 2 + 4 - a 2 a

Ultimo passo chegando!

Passo 4

Perfeito galera, pra fechar, a gente aplica o limite a → 0 :

lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2   = lim a → 0 + ⁡ - 1 2 ln ⁡ 2 + 3 + 1 2 ln ⁡ 2 + 4 - a 2 a

lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2   = - 1 2 ln ⁡ 2 + 3 + 1 2 ∙ lim a → 0 + ⁡ ln ⁡ 2 + 4 - a 2 a

Nota o seguinte galera, o limite que sobrou:

lim a → 0 + ⁡ ln ⁡ 2 + 4 - a 2 a

Quando a → 0 , vai dar:

lim a → 0 + ⁡ ln ⁡ 2 + 4 - a 2 a = ln ⁡ 2 + 4 - 0 + 0 + = ln ⁡ 4 0 + = ln ⁡ + ∞ = + ∞

Portanto:

lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2   = - 1 2 ln ⁡ 2 + 3 + 1 2 ∙ ∞

lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2   = + ∞

Resposta

lim a → 0 + ⁡ ∫ a 1 d x x 4 - x 2   = + ∞

A integral imprópria é divergente.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como vimos na seção 3.8, uma substância radioativa decai exponencialmente: a massa no tempo t é m t = m 0e k t , onde m ( 0 ) é a massa inicial e k , uma constante negativa. A vida média M de um átomo
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 ∞ x arctg ⁡ x 1 + x 2 2 d x
Seja f ( t ) a função densidade de probabilidade para o tempo que você leva para ir à escola de manhã, com t medido em minutos. Expresse as seguintes probabilidades como integrais. A probabilidade de
Seja f x = x e - x se x ≥ 0 e f x = 0 se x0 .Verifique que f é uma função densidade de probabilidade.Calcule P ( 1 ≤ X ≤ 2 ) .