Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 32
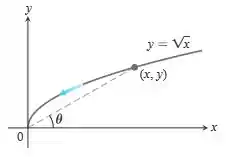
Encontre uma parametrização para a curva com ponto final utilizando o ângulo u na figura a seguir como parâmetro.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Da figura do enunciado, podemos escrever
Portanto,
Usando a equação (1) substituindo em é
Desenvolvendo os termos
Portanto,
Passo 2
Substitua esta expressão por x na Equação 1
Da figura podemos ver que , mas vamos excluir , porque torna indefinido.
Resposta
Exercícios de Livros Relacionados
Desenhe as lemniscatas nos Exercícios 13-16. Quais simetrias essas curvas têm? r 2 = 4 cos 2 θ
Desenhe as lemniscatas nos Exercícios 13-16. Quais simetrias essas curvas têm? r 2 = - cos 2 θ
Desenhe as lemniscatas nos Exercícios 13-16. Quais simetrias essas curvas têm? r 2 = - sen 2 θ
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para