Subtração de Frações

Ao escrevermos uma fração estamos escrevendo uma divisão de uma maneira diferente. E quando escrevemos uma ou mais frações podemos aplicar operações nessas frações. Aqui vamos entender como realizar a subtração de frações.

Toda fração é formada por um numerador e um denominador:

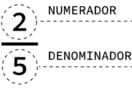
Numerador é aquele que fica em cima e denominador é aquele que fica em baixo. Nós sempre teremos que prestar atenção nesses dois números quando formos fazer operações com frações. No exemplo a cima podemos dizer que estamos com dois pedaços de algo que está dividido em 5 partes, e lemos essa fração como “dois quintos”. Existem dois casos possíveis quando vamos operar com frações:

1. Frações com denominadores iguais

O caso mais simples é o caso em que vamos subtrair duas frações com um mesmo denominador. E o exemplo clássico é aquele das fatias de pizza:

Ana e João pediram uma pizza que veio dividida em 8 pedaços Ana comeu 2 pedaços e João comeu 3 pedaços, qual a fração de pizza que sobrou?

Nesse exercício em todo momento nós temos o mesmo denominador, porque em todo momento estamos falando de uma pizza dividida em 8 pedaços, e portanto apenas precisamos operar os numeradores porque já estamos com um denominador comum:

$$\underset{Apizzainteira}{\underbrace{\frac{8}{8}}}-\underset{\begin{array}{c}DoispedaçosdeAna\\ numtotalde8pedaços\end{array}}{\underbrace{\frac{2}{8}}}-\underset{\begin{array}{c}TrêspedaçosdeJoão\\ numtotalde8pedaços\end{array}}{\underbrace{\frac{3}{8}}}=\underset{\begin{array}{c}Restaram3pedaçosdapizza\\ deumtotalde8pedaços\end{array}}{\underbrace{\frac{3}{8}}}$$

Logo restaram “três oitavos” da pizza.

2. Frações com denominadores diferentes

Nesse caso vamos ter que igualar os denominadores antes de poder operar com os numeradores. É bem simples, vamos dar uma olhada.

A vovó Nice fez um bolo para seus netinhos. No primeiro dia Enzo comeu um nono do bolo e Valentina comeu dois décimos do bolo. No dia seguinte Enzo comeu dois sextos do que havia restado do bolo e Valentina comeu quatro décimos. Quanto restava do bolo no final do primeiro dia e do segundo dia? Responda com frações.

Para resolver esse probleminha, nós vamos fazer subtrações de frações, mas temos que nos atentar para os denominadores, repare:

Vou considerar que no primeiro dia, existia um bolo inteiro:

$$1bolo$$

E vamos lembrar que Enzo e Valentina comeram respectivamente:

$$\frac{1}{9}doboloe\frac{2}{10}dobolo$$

Então teríamos:

$$\underset{BoloInteiro}{\underbrace{1}}-\underset{\begin{array}{c}PedaçoqueoEnzocomeu\\ noprimeirodia\end{array}}{\underbrace{\frac{1}{9}}}-\underset{\begin{array}{c}Pedaçoqueavalentinacomeu\\ noprimeirodia\end{array}}{\underbrace{\frac{1}{10}}}$$

Para calcular o resultado, primeiro teremos que encontrar o mínimo multiplicador comum entre (1, 9, 10), vamos fazer isso:

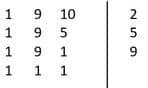
O que eu fiz foi encontrar os menores divisores em comum desses números, repare que eles não têm nenhum divisor em comum, logo o nosso resultado $2\times 5\times 9$ vai ser a mesma coisa que multiplica $10\times 9$, então nosso divisor comum será:

$$2\times 5\times 9=10\times 9=90$$

Então o denominador que gostaríamos de usar nesse primeiro cálculo é o $90,$ então vamos igualar os denominadores:$$$$\frac{1}{1_{/\times 90}}-\frac{1}{9_{/\times 10}}-\frac{1}{{10}_{/\times 9}}=\frac{90}{90}-\frac{10}{90}-\frac{9}{90}=\frac{71}{90}$$

Então do primeiro dia restou setenta e um noventa avos do bolo. E temos que continuar nossos cálculos para descobrir quanto os netos comeram no segundo dia.

No segundo dia Enzo e Valentina comeram respectivamente:

$$\frac{2}{6}doboloe\frac{3}{10}dobolo$$

Então teríamos:

$$\underset{\begin{array}{c}Oquereestoudo\\ primeirodiado\\ bolo\end{array}}{\underbrace{\frac{71}{90}}}-\underset{\begin{array}{c}OqueoEnzocomeu\\ nosegundodia\end{array}}{\underbrace{\frac{2}{6}}}-\underset{\begin{array}{c}OqueaValentina\\ comeunosegundodia\end{array}}{\underbrace{\frac{3}{10}}}$$

Podemos reparar que $90$é múltiplo de 6 $(6\times 15=90)$ e de $10(10\times 9=90)$, logo podemos encontrar um denominador comum entre essas três frações que será o próprio 90. Se fossemos calcular o MMC entre esses três números encontraríamos $150$, repare:

$$2\times 3\times 5\times 5=150$$

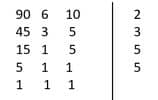
Poderíamos trabalhar também com o denominador sendo 150, mas não precisamos trabalhar com números tão altos, se já sabemos que $90$ é um múltiplo de $6$ e de $10:$

$$\frac{71}{90}-\frac{2}{6_{/\times 15}}-\frac{3}{{10}_{/\times 9}}=\frac{71}{90}-\frac{30}{90}-\frac{27}{90}=\frac{14}{90}$$

Dessa forma no final dos dois dias restavam apenas $\frac{14}{90}$(catorze noventa avos) do bolo.

Subtração de Fração é um assunto inicial de matemática e é essencial para continuar os estudos nessa área, se ainda ficou com alguma duvida nessa teoria, da uma olhada no nosso site para ver esse e muitos outros assuntos tanto de Matemática, quanto de outras matérias de exatas! Além disso faço uma recomendação pessoal para dar um revisada em tabuada caso não tenha se sentido muito familiarizado com as contas que fizemos nesses exercícios!