Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformada de Laplace da Função Degrau

Ver Todos os Exercícios

Teoria

Introdução

Olá, galerinha! Vamos ver agora qual é a Transformada de Laplace da Função degrau. Se lembra dela? Para você que disse não, aqui vai um resumo:

A função degrau é uma função que antes de certo valor c , ela vale 0 , e depois desse c ela dá um salto virando 1 . Tá confuso ainda? Olha o gráfico como é:

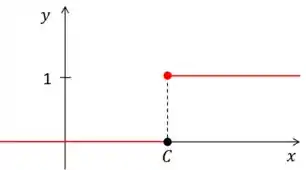
Repara que o traço vermelho forma uma escadinha. Por isso, ela se chama função degrau, justamente por ter o formato de um, saca? E como se representa essa função:

u c t = 0 , t < c 1 , t ≥ c

Ou seja, se eu tenho uma função u 2 t , significa a que minha função vale zero até o x = 2 e a partir dali ela valerá 1 . Repara que o gráfico é a mesma coisa do que desenhei acima. Eu só substitui o c por 2 ,

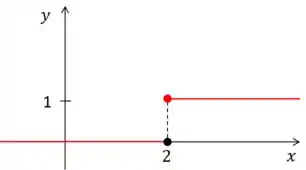
Mas agora que vem o mistério: Como eu faço a Transformada de Laplace disso?

Transformada de Laplace da Função Degrau

Então, galerinha, essa transformada é uma que a gente tem que memorizar. Então já adiciona ela naquela tabelinha esperta com outras transformadas.

Acabando com o mistério, a transformada de Laplace da Função Degrau é a seguinte,

L u c t = e - s c s

Ficou um pouco abstrato né? Mas vamos ver agora como aplicar essa transformada ai com alguns exemplos:

Exemplo: Vamos calcular a Transformada de Laplace da função abaixo, y = 2 u 1 t - u 2 t

Repara que nosso y é a diferença de duas funções degraus, multiplicado por dois. Você não precisa entender como é essa função para resolver a transformada, mas vou colocar o gráfico dela aqui embaixo só para você visualizar,

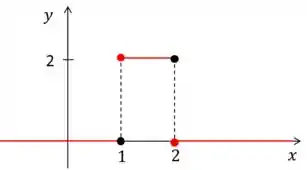
Ok, agora vamos ao que o problema pede que é a transformada! A gente pode aplicar as propriedades da Transformada de Laplace de boas aqui,

L y = 2 L u 1 t - u 2 t

= 2 L u 1 t - L u 2 t

Pronto, agora vamos usar aquela formulazinha que eu pedi para você anotar na sua tabelinha,

L y = 2 e - s s - e - 2 s s

Viu? Bem simples. Agora vamos complicar um pouco as coisas.

Transformada de Laplace de uma função multiplicada por um degrau unitário

Galera, agora, vamos multiplicar a nossa função degrau por outra função. Não entendeu? Olha o exemplo abaixo,

Exemplo: Como calcular a transformada de

g t = u 0 t sen ⁡ t

Repara aqui que temos um degrau multiplicado pela função seno.

Então, galerinha, quando a gente tiver um caso assim, nós vamos usar a seguinte fórmula,

L u c t f t - c = e - c s L { f t }

Agora vamos aplicar para o exemplo! A nossa parte degrau a gente consegue achar no nosso g ( t ) é o u 0 t . Mas quem seria essa parte f t - c que apareceu dentro da minha transformada? Então, é o nosso sen ⁡ t . Então fica assim,

L u 0 t sen ⁡ t

Mas repara que devemos escrever f t = sen ⁡ t como sendo f t - c . Então ficaria assim,

L u 0 t sen ⁡ t - c

No nosso caso c = 0 , então podemos afirmar que sen ⁡ t = sen ⁡ t - 0 . Então a transformada fica assim,

L u 0 t sen ⁡ t - 0 = e - 0 . s L sen ⁡ t = 1 s 2 + 1

Essa fórmula é conhecida por teorema do deslocamento.

Então, galerinha, quando aparecer uma situação assim, faremos o seguinte passo a passo:

  1. A gente tem que ter um degrau num ponto c e uma função deslocada de c unidades (é escrever f ( t - c ) ). Tem que ser o mesmo c !
  2. Achar a f ( t )
  3. Transformar f ( t )
  4. Multiplicar a transformada por e - c s

Vamos ver mais um exemplo para entender isso tudo melhor!

Exemplo: Calcule a Transformada de Laplace da função y dada por

y = 0 ;       t < 2 t - 2 2 ;       t ≥ 2    

Passo 1: Vamos desenhar essa função:

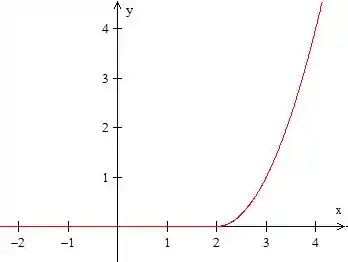
Repara que nós temos uma função que vale zero até t = 2 e, depois disso, vale t - 2 2 . Temos, então, uma função degrau que começa em t = 2 multiplicada por t - 2 2 , ou seja:

y t = u 2 t t - 2 2

Isso quer dizer que:

Antes de t = 2 , temos

0 × t - 2 2 = 0

Depois de t = 2 , temos,

1 × t - 2 2 = t - 2 2

Repara que é exatamente o que o problema pediu. Beleza, precisamos agora calcular a transformada dessa função.

Passo 2: Encontrar f ( t ) a partir de f ( t - c ) .

Queremos então:

L y = L u 2 t - 2 2

Lembra da nossa fórmula,

L u c f t - c = e - c s L f t

Substituindo,

L { u 2 t - 2 2 ⏟ f t - 2 } = e - 2 s L f t

Mas como achar f t ? Comparando a expressão do teorema com a que a gente achou, vamos ter:

f t - 2 = t - 2 2

Para f ( t - 2 ) se tornar f ( t ) ? Basta eliminar o - 2 daí:

f t = t 2

Passo 3: Calcular L f t

Lá da nossa tabelinha, sabemos que

L t 2 = 2 s 3

Substituindo esse valor, temos:

L u 2 t - 2 2 = e - 2 s L f t         →

L u 2 t - 2 2 = e - 2 s 2 s 3

Pronto! Resolvemos mais uma Transformada de Laplace.

Agora se você tiver pensando: “Mas e se a função f não estiver deslocada para ( t - c ) ?”

Ela tem que ser função de ( t - c ) para você aplicar essa fórmula! Então, você terá que manipular a função para fazer aparecer esse t - c .

Calma que vamos ver isso melhor nos exercícios, então corre lá!

Transformada de Laplace de uma função multiplicada por um degrau unitário

Exercícios Resolvidos

Exercício Resolvido #1

William E. Boyce, Equações diferenciais Elementares e problemas de valores de contorno, 8ªed. Rio de Janeiro: LTC, 2006, pp. 178, exercício 9

Encontre a transformada de Laplace da função dada.

f t = 0 ,                                                 t < π t - π ,             π ≤ t < 2 π 0 ,                                             t ≥ 2 π

Passo 1

Precisamos escrever y ( t ) em função de u c t , para podermos calcular a transformada.

Vamos primeiro desenhar essa função:

Repare que isso é o mesmo que:

A função da figura da esquerda vale zero até t = π e depois tem valor igual à equação da reta, ( t - π ) , então, podemos escrevê-la como u π t [ t - π ] .

A função da direita vale zero até t = 2 π e depois vale ( t - π ) . Então, podemos escrevê-la como u 2 π t [ t - π ] .

Como a função do problema é a diferença entre essas duas, temos:

y t = u π t t - π - u 2 π t [ t - π ]

Precisamos calcular a transformada disso aí agora. Como temos dois u c ’s diferentes, vamos calcular cada transformada separadamente.

L y t s = L u π t - π s - L u 2 π t - π s

Passo 2

  1. Para L u π t - π s

    2. Precisamos encontrar f ( t ) a partir de f ( t - c ) . Temos a seguinte fórmula:

    L [ u π t - π ⏟ f t - π ] ( s ) = e - π s L [ f t ] ( s )

    Sabemos que

    f t - π = t - π

    Para f ( t - π ) se tornar f ( t ) , temos que substituir t por ( t + π ) , não é? Então vamos somar π onde tem t , olha só:

    f t = t + π - π = t

    Pronto, descobrimos f ( t ) , agora basta substituir na fórmula:

    L u π t - π s = e - π s L t ( s )

  2. Para L u 2 π t - π s

Precisamos encontrar f ( t ) a partir de f ( t - c ) . Temos a seguinte fórmula:

L [ u 2 π t - π ⏟ f t - 2 π ] ( s ) = e - 2 π s L [ f t ] ( s )

Sabemos que

f t - 2 π = t - π

Para f ( t - 2 π ) se tornar f ( t ) , temos que substituir t por ( t + 2 π ) , então vamos fazer isso para os dois lados da equação:

f t = t + 2 π - π = t + π

Pronto, descobrimos f ( t ) , agora basta substituir na fórmula:

L u 2 π t - 2 π s = e - 2 π s L t + π ( s )

Nota: Cuidado! As duas funções degrau u π e u 2 π estavam multiplicadas pela mesma função ( t - π ) , mas a f ( t ) que encontramos para cada uma delas era diferente. Isso acontece porque para cada caso chamamos essa função de f ( t - c ) e esse “ c ” não é o mesmo nos dois casos.

Passo 3

Temos, então:

L y t s = e - π s L t ( s ) ⏟ L u π t - π s - e - 2 π s L t + π ( s ) ⏟ L u 2 π t - 2 π s

Agora é só calcular as transformadas!

L t s = 1 s 2

L t + π s = 1 s 2 + π s = 1 + π s s 2

Substituindo esses valores, temos:

L y t s = e - π s s 2 - e - 2 π s 1 + π s s 2

Resposta

e - π s s 2 - e - 2 π s 1 + π s s 2

Exercício Resolvido #2

Função Degrau

Calcule a transformada de Laplace da função

f t = cos ⁡ 2 t ,     0 ≤ t < π cos ⁡ 2 t + s e n   ( t - π ) ,     t ≥ π

Passo 1

Vamos primeiro reescrever a função f ( t ) , observando que a parte do s e n   ( t - π ) só é introduzida para t ≥ π . Assim, temos:

f t = cos ⁡ 2 t + s e n   t - π u π t

Passo 2

Então, para calcular a transformada, sabemos que:

L cos ⁡ 2 t = s s 2 + 4

L sen ⁡ t = 1 s 2 + 1

Mas, com o deslocamento de π :

  L sen ⁡ t - π u π ( t ) = 1 s 2 + 1 e - π s

Passo 3

Combinando os resultados:

L { f t } = L { cos ⁡ 2 t } + L { s e n   t - π u π t }

L f t = s s 2 + 4 + e - π s s 2 + 1

Resposta

L f t = s s 2 + 4 + e - π s s 2 + 1

Exercício Resolvido #3

UFRJ - Cálculo 4 - P1 2014.1 - 3ª

Calcular a transformada de Laplace da função f definida por

f t = 0 ,                   s e   0 ≤ t < π / 2 e t sen ⁡ t ,     s e   t ≥ π / 2

Passo 1

Precisamos de um esboço para escrevermos f ( t ) como função degrau. O gráfico dessa função é um negócio assim:

Você sabia disso? Pois é, eu também não, acabei de descobrir : ) A verdade é que não precisamos saber como é a função e t sen ⁡ t , só precisamos saber onde ela começa, para podermos raciocinar.

Então, vamos usar um desenho qualquer para essa função, ok? Pois não fazemos ideia de como ela seja:

Passo 2

Agora vamos escrever f ( t ) como função degrau. Como temos uma função que vale 0 até t = π / 2 e passa a valer e t s e n   t a partir de t = π / 2 , podemos escrever o seguinte:

f t = u π 2 t [ e t sen ⁡ t ]

Isso quer dizer que:

p a r a   t < π / 2       f ( t ) = 0 × e t sen ⁡ t = 0 p a r a   t ≥ π / 2     f t = 1 e t sen ⁡ t = e t sen ⁡ t  

Pronto, isso que queremos!

Passo 3

Agora vamos calcular L f t ( s ) , como o problema pediu. Temos o seguinte:

L u c g t - c s = e - c s L g t ( s )

Aplicando para o nosso problema:

L [ u π / 2 e t sen ⁡ t ⏟ g ( t - π / 2 ) ] s = e - π s / 2 L g t ( s )

Precisamos, então, achar g ( t ) . Temos o seguinte:

g t - π / 2 = e t sen ⁡ t

Então, para encontrarmos g ( t ) temos que somar π / 2 onde tem t :

g t = e t + π / 2 sen ⁡ t + π 2

Como:

sen ⁡ t + π 2 = sin ⁡ t cos ⁡ π 2 + sin ⁡ π 2 cos ⁡ t = cos ⁡ ( t )

g t = e t + π / 2 cos ⁡ ( t )

Assim, temos:

L f t s = L [ u π 2 e t sen ⁡ ( t ) ] s = e - π s / 2 L e t + π / 2 cos ⁡ ( t ) ( s )

Passo 4

Precisamos agora resolver essa expressão. Vamos rearrumar isso aqui:

L f t s = e π 2 ( 1 - s ) L e t cos ⁡ ( t ) ( s )

Sabemos do seguinte:

L cos ⁡ t s = s s 2 + 1

Como temos uma exponencial multiplicando o cosseno, essa transformada será deslocada. Vamos usar a seguinte fórmula:

L e c t f t s = L f t ( s - c )

L e t cos ⁡ t s = L cos ⁡ t s - 1 = s - 1 ( s - 1 ) 2 + 1

Substituindo esse valor, temos:

L f t s = e π 2 ( 1 - s ) s - 1 ( s - 1 ) 2 + 1

Resposta

L f t s = e π 2 ( 1 - s ) s - 1 ( s - 1 ) 2 + 1

Exercício Resolvido #4

William E. Boyce, Equações diferenciais Elementares e problemas de valores de contorno, 8ªed. Rio de Janeiro: LTC, 2006, pp. 178, exercícios 2 e 11

Esboce o gráfico da função dada no intervalo t ≥ 0 e encontre sua transformada de Laplace.

f t = t - 3 u 2 t - t - 2 u 3 ( t )

Passo 1

Vamos primeiro desenhar essa função. Temos o seguinte:

Juntando todas essas informações, temos:

  1. De 0 a 2 , y = 0 - 0 = 0
  2. De 2 a 3 , y = t - 3 - 0 = t - 3
  3. De 3 em diante, y = t - 3 - t - 2 = - 1

Temos, então, o seguinte gráfico:

Passo 2

Agora vamos calcular a transformada dessa função.

L t - 3 u 2 t - t - 2 u 3 ( t ) s = L ( t - 3 ) u 2 t s - L ( t - 2 ) u 3 t s

Sabemos que

L u c f t - c s = e - c s L f t ( s )

  1. Para a primeira transformada

    2. L ( t - 3 ) u 2 t s = e - 2 s L f t ( s )

    Temos

    f t - 2 = t - 3

    Logo

    f t = t + 2 - 3 = t - 1

    Isso nos dá

    L ( t - 3 ) u 2 t s = e - 2 s L t - 1 ( s )

  2. Para a segunda transformada

L ( t - 2 ) u 3 t s = e - 3 s L f t ( s )

Temos

f t - 3 = t - 2

Logo

f t = t + 3 - 2 = t + 1

Isso nos dá

L ( t - 2 ) u 3 t s = e - 3 s L t + 1 ( s )

Passo 3

Temos, então, o seguinte:

L f t s = e - 2 s L t - 1 s - e - 3 s L t + 1 ( s )

Vamos resolver essa expressão.

L t - 1 s = 1 s 2 - 1 s = 1 - s s 2

L t + 1 s = 1 s 2 + 1 s = 1 + s s 2

Substituindo esses valores:

L f t s = e - 2 s 1 - s s 2 - e - 3 s 1 + s s 2

Resposta

e - 2 s 1 - s s 2 - e - 3 s 1 + s s 2