Uma Câmara de Poeira (, , ), fabricada com chapas de aço, trata de um efluente gasoso industrial contendo partículas () em suspensão. A Distribuição de Tamanho das partículas segue o modelo RRB ( e ). Em razão de graves problemas de corrosão das chapas na região próxima à saída da câmara, sugere-se reduzir seu comprimento para 2,5 m. Supondo-se inalteradas as demais variáveis envolvidas, e supondo-se ainda que as propriedades físicas do gás em questão sejam idênticas às do ar a e e que as dez restrições da Lei de Stokes sejam respeitadas, pede-se:
- Calcule a diminuição percentual da eficiência global de coleta da câmara, caso a modificação seja implementada.
Passo 1
A questão pede para calcularmos os a diminuição percentual da eficiência. Para isso, precisamos encontrar a eficiência com a Câmara de Poeira nas duas dimensões.
Primeiramente, vamos organizar os dados que a questão forneceu:
Dimensões da Câmara de Poeira original
Largura
Altura
Comprimento
Dimensões da Nova Câmara de Poeira
Largura
Altura
Comprimento
Foi dado também a vazão da câmara de poeira, que vai ser super útil para esse exercício se for em segundos:
A partir do dado , conseguimos achar o .
Como o ar está a e , podemos retirar suas propriedades de tabelas, nessas condições, e veremos que:
Passo 2
Beleza, mas e agora que já temos tudo isso como calculamos a eficiência global quando temos o modelo de distribuição de tamanho? Bora fazer uma pequena revisão do tópico de Eficiência!
Lembram da curva de eficiência de distribuição granulométrica para um dado diâmetro?
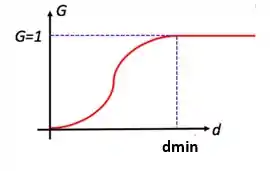
Já vimos que a Eficiência total é dada por:
Essa área dessa curva para todos os diâmetros pode ser descrita também pela seguinte equação em função de :
Essa equação aí representa a eficiência global, pois é como se calculássemos a eficiência em cada diâmetro da nossa amostra, concorda comigo?
E tanto essa integral quanto esse podem ser calculados pelo modelo RRB, que foi dado no problema. Substituindo pelos parâmetros dados o RRB fica com essa carinha aqui:
E colocando ele dentro da integral (já que ele fornece o valor de ), temos que:
Obs: Não se assusta que na sua prova já deve vir um formulário com essa integral resolvida.
Então, para achar o , precisamos encontrar o equivalente para a câmara de poeira original e a nova, considerando as restrições de Stokes 😊
Passo 3
Vamos calcular então o que precisamos para as duas câmaras de poeira:
Agora, como sabemos que o modelo é RRB, conseguimos encontrar o para cada uma das câmaras de poeira, substituindo os valores que acabamos de achar.
E, por fim, podemos jogar as integrais da eficiência das duas câmaras de poeira na calculadora:
Passo 4
Agora que temos as duas eficiências podemos calcular a redução das eficiências: