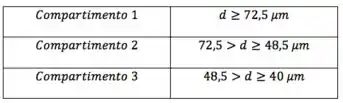
O separador de poeiras opera em compartimentos, como mostra o esquema abaixo representado. Estimar a faixa granulométrica das partículas retidas com eficiência granulométrica igual a em cada compartimento, sabendo-se que a vazão de gás (ar a ) é , a densidade das partículas é e a sua esfericidade é .
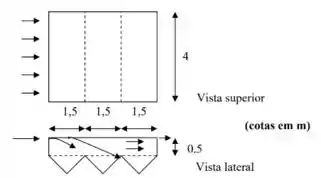
Passo 1
Isso de compartimentos pode parecer um pouco enrolado na primeira vez que a gente olha, mas de enrolado não tem nada; o que vamos ter que fazer é quebrar nossa análise: primeiro, olhamos só para o primeiro compartimento (ignora o resto!), ou seja, para e vemos qual o diâmetro fica retido com eficiência de , isto é, , já que estou falando de diâmetro. Depois, a gente olha até o final do segundo compartimento, isto é, do começo até , e vê qual partícula tem para esse comprimento. Por último, olhamos pra câmara como um todo. O , vamos “variar”, mas as outras dimensões são constantes:
Repara, agora, que o enunciado não deu informação de nenhum diâmetro. SEEEE, ele tivesse dito quem é o , ou o , ou qualquer outro , poderíamos PENSAR em usar:
Mas não foi o caso. Vamos ficar com:
Já sacou que vamos precisar de e precisar usar para as partículas né? Mas para calcular , precisamos de , que o enunciado não deu diretamente. MASSSSS, sabemos que as condições do gás então dá pra calcular. Antes de qualquer coisa, precisamos definir o sistema de unidade que vamos usar. Vou escolher o SI porque já tem muita coisa no SI no enunciado. Agora, assumindo gás ideal, vale:
Como o número de moles, , é massa sobre massa molecular média (média porque ar atmosférico é uma mistura):
Isolando , que é a densidade, :
Sabemos que e (converti porque tem que jogar em temperatura absoluta na fórmula). Falta e , mas isso é de boas, são tabelados.
E, pelas unidades que estamos usando, escolhemos:
Daí:
Também para , precisamos de . Precisamos ir atrás de uma tabela com do ar versus temperatura, nessa pressão de . Daí, achamos:
Quanto a , é só lembrar que vazão volumétrica é velocidade vezes área transversal do equipamento, daí:
Passo 2
Analisando o primeiro compartimento, queremos a dele, que está associada com , certo? Jogando tudo isso que sabemos na fórmula:
E qual é o diâmetro que tem essa ? Coelho e Massarani! Vamos pelo caminho de , já que temos a velocidade.
Repara que eu converti para o SI, daí esse . Agora, para obter o , uso:
E, para isso, preciso antes calcular e :
Daí:
Usando a fórmula de
Esse é o do primeiro compartimento, mas repara que o enunciado pede “Estimar a faixa granulométrica das partículas retidas com eficiência granulométrica igual a em cada compartimento”. Agora, lembra que todos os diâmetros maiores do que possuem , isto é, possuem eficiência granulométrica igual a ? Então, a resposta para esse primeiro compartimento é:
Passo 3
Agora, vamos ver qual partícula é a se considerarmos até o fim do segundo compartimento, isto é, :
Aplicando , lembrando que, como não mudamos a morfologia da partícula, e são os mesmos:
Aplicando a fórmula pra :
Então, tudo que tiver vai sedimentar com eficiência de dentro desses metros. Acontece que o enunciado perguntou qual a faixa que sedimenta no segundo compartimento, isto é, em , e tudo que tinha sedimentou no primeiro compartimento, isto é, . Daí, a faixa que, efetivamente, sedimenta com no segundo compartimento é:
Passo 4
Agora, temos que considerar o comprimento todo, ou seja,
Aplicando , lembrando que, como não mudamos a morfologia da partícula, e são os mesmos:
Aplicando a fórmula pra :
Seguindo a mesma lógica do passo anterior, partículas com sedimentam antes da entrada do terceiro compartimento, daí o que realmente fica no terceiro compartimento é:
Resposta