Duas cargas elétricas puntiformes, e estão fixas, separadas de , no vácuo. No ponto , a de , conforme mostra a figura abaixo:
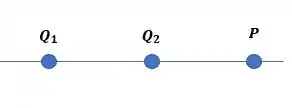
O módulo do vetor campo elétrico, em unidade do sistema internacional, vale?
(Dado: constante eletrostática igual a )
- Zero
Passo 1
O enunciado nos fala sobre a distância entre as cargas ser igual a :
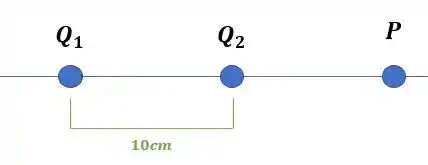
Enquanto o ponto fica a uma distância de da carga :
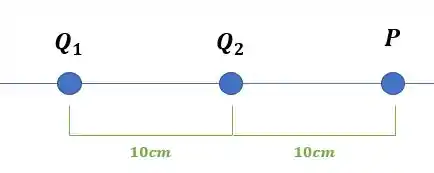
Passo 2
Considerando apenas a primeira carga que é negativa, sabemos que o campo elétrico apontará em sua direção, dessa forma:
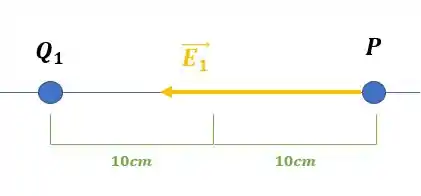
Enquanto seu módulo seguirá a fórmula:
No caso, como já sabemos a direção, necessitamos saber apenas o módulo do campo elétrico:
Sabemos o valor da constante eletrostática :
Substituindo na equação, temos:
Sabemos também que o valor da carga é igual a:
Como desejamos o módulo da carga, podemos desconsiderar o sinal negativo:
Aplicando na equação, ficamos com:
Enquanto a distância será igual a soma entre a distância de até e a distância de até o ponto :
Sabemos que devemos sempre realizar as contas com o valor da distância em metros, logo:
Substituindo o valor na equação, temos:
Passo 3
Agora que já montamos o cálculo do campo elétrico gerado pela carga , vamos realizar esse cálculo:
Primeiro vamos elevar o número ao quadrado:
Substituindo essa informação no cálculo:
Vamos fazer a multiplicação entre as potências de , para isso, mantemos a base e somamos os expoentes:
Logo:
Fazendo a divisão entre potências de , vamos manter a base e subtrair os expoentes:
Ficamos com:
Fazendo a multiplicação e divisão entre os números, temos:
Ou seja:
Não esquece a unidade, tudo bem? Então ficamos com esse primeiro campo elétrico:
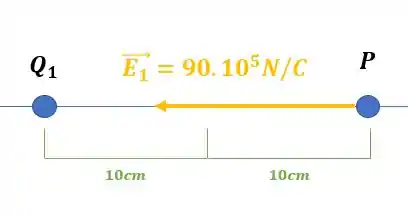
Agora vamos fazer a mesma coisa para descobrir o campo elétrico gerado pela carga , você não tinha esquecido dela, né?
Passo 4
Considerando apenas a segunda carga que é positiva, sabemos que o campo elétrico apontará de dentro para fora da carga, dessa forma:
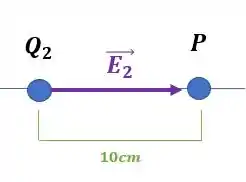
Enquanto seu módulo seguirá a fórmula:
No caso, como já sabemos a direção, necessitamos saber apenas o módulo do campo elétrico:
Sabemos o valor da constante eletrostática :
Substituindo na equação, temos:
Sabemos também que o valor da carga é igual a:
Como a carga é positiva, seu módulo é igual ao seu valor:
Aplicando na equação, ficamos com:
Enquanto a distância será igual a distância de até o ponto :
Sabemos que devemos sempre realizar as contas com o valor da distância em metros, logo:
Substituindo o valor na equação, temos:
Passo 5
Agora que já montamos o cálculo do campo elétrico gerado pela carga, vamos realizar esse cálculo:
Primeiro vamos elevar o número ao quadrado:
Substituindo essa informação no cálculo:
Vamos fazer a multiplicação entre as potências de , vamos manter a base e somar os expoentes:
Logo:
Fazendo a divisão entre potências de , vamos manter a base e subtrair os expoentes:
Ficamos com:
Fazendo a multiplicação e divisão entre os números, temos:
Ou seja:
Não esquece a unidade, tudo bem? Então ficamos com esse segundo campo elétrico:
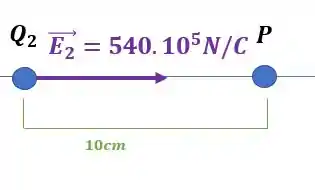
Agora vamos colocar os dois campos ao mesmo tempo, para saber qual é o efeito!
Passo 6
Podemos ver que cada carga causa um campo elétrico no ponto :
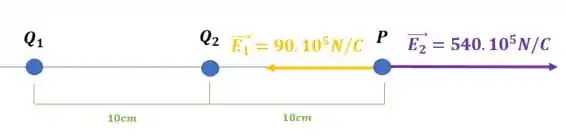
Como eles são opostos, apontam para lados opostos, temos que ver quem tem o maior módulo, nesse caso é o segundo campo elétrico:
E para encontrar o valor do módulo do campo resultante, vamos subtrair os valores dos campos:
Substituindo os valores:
Também podemos reescrever como:
Ou seja, chegamos na nossa reposta final!
Resposta
c)