Considere um ciclo de turbina a gás ideal com dois estágios de compressão e dois estágios de expansão. A razão de pressão em cada estágio do compressor e da turbina é de 3. O ar entra em cada estágio do compressor a 300K e em cada estágio da turbina a 1200K. Considerando calores específicos constantes, determine a relação entre a potência necessária para acionar o compressor e a potência desenvolvida pela turbina, assim como o rendimento térmico do ciclo para o caso em que há um regenerador com eficiência de 75%. Dados: ;
Passo 1
Primeiro é interessante colocar esse problema num diagrama para ser mais fácil de visualizar. Se lembra quando estamos trabalhando com mais de um estágio ele parece um serrote? Então vai ficar mais ou menos assim:
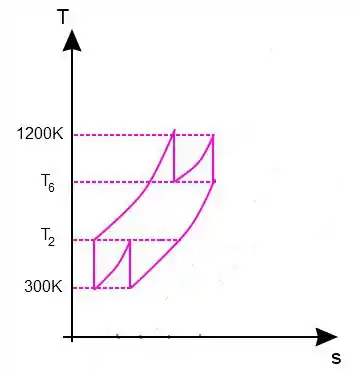
Agora, diferentemente do problema anterior o calor trocado entre e é o calor trocado no regenerador. Portanto, o cálculo do vai ser um pouquinho diferente.
Passo 2
Como os processos nos compressores e nas turbinas são isentrópicos a relação entre pressão e temperatura é dada por
Como nos foi dado a relação e um as temperaturas de entrada no compressor e na turbina, podemos achar a temperatura de saída de cada um.
Temos de lembrar, também que
Calculando a temperatura de saída do compressor
Passo 3
Vamos fazer a mesma coisa para a saída da turbina
Passo 4
Os cálculos da potência e calor todos dependem da variação da entalpia. Para o compressor e a turbina, por ser uma isentrópica, a variação da entalpia é igual a . O calor fornecido numa isobárica é dado, também, por . Como são duas turbinas e dois compressores:
Mas agora parte desse calor recebido pelo sistema é regenerado ou seja
E o calor regenerado é dado por
Passo 5
O rendimento térmico do ciclo para o caso em que há um regenerador de 75% de eficiência é
Resposta
O rendimento térmico do ciclo para o caso em que há um regenerador de 75% de eficiência é