Um ciclone Lapple deve processar uma suspensão gasosa diluída de ar atmosférico, visando a separação de partículas de com eficiência de A densidade do sólido é igual a 2100 . A pressão da alimentação é de e a temperatura é .
a) Dimensione o ciclone e determine a vazão que pode ser processada.
b) Qual a potência de um soprador requerida, sendo a eficiência do soprador igual a 60%?
Passo 1
A primeira coisa que temos que buscar no enunciado ao trabalhar com ciclones é qual a família; nesse caso, temos um ciclone Lapple. Daí, daquela tabela lá da teoria:
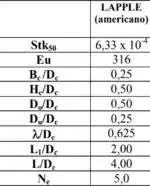
Como as relações entre as dimensões de um ciclone são tabeladas, basta determinar o e, sabendo de qual família se trata, nosso dimensionamento estará de boas.
E nós podemos obter o por:
Mas repara que ainda não temos algumas outras variáveis que entram aí. O que a gente sabe é que:
- Tenho as condições do gás, daí posso calcular e pesquisar sobre
- Através da informação da eficiência da partícula de , posso calcular o
- e posso escrever e em função de
Dessa forma, como o valor de é tabelado, só sobra uma variável a determinar e aí tiramos . Aí, voltamos e calculamos também.
Na letra b, vamos precisar usar o número de Euler para calcular a queda de pressão no ciclone e depois, pra calcular a potência, é só usar:
E, como só tem um ciclone, , em que é a vazão calculada no item a.
Pra esse exercício, vamos usar SI já que temos alguns dados nesse sistema. Mas você pode fazer como preferir!
Ah! Uma coisa: esse “suspensão gasosa DILUÍDA” nos diz que não precisamos fazer correção de concentração pra velocidade terminal.
Passo 2
Bora começar calculando o diâmetro de corte, . De “separação de partículas de com eficiência de ”, sabemos que, para , . Daí usando a expressão de para ciclones:
Eu vou resolver isso na HP Prime. Tem que ir na tecla que tem uma maletinha, depois “Solve”, depois “Zeros”. E você vai precisar lançar a forma homogênea da equação, que é quando está igualada a zero; é só passar o pro outro lado:
Mas esse comando “zeros” já entende que está igualado a zero; daí você só lança a parte da esquerda. Na sua tela, vai aparecer:
Aí, a HP me retornou:
Ou seja, ou . Como estamos falando de diâmetro, não faz sentido ser negativo. Daí:
Com podemos ir pro e calcular . Mas antes, precisamos das propriedades físicas do fluido.
Passo 3
Assumindo gás ideal, vale:
Como:
Rearranjando:
Precisamos da temperatura em escala absoluta; passando pra Kelvin:
Daí:
Pra do ar atmosférico, vamos considerar que ele é formado por 80% de gás nitrogênio () e 20% por gás oxigênio ().
Daí:
Indo atrás da viscosidade nessas condições:
Passo 4
Agora repara que:
Temos quase tudo, mas ainda falta a vazão . Lembra que:
Não temos nenhuma informação sobre ; nesses casos, como disse lá na teoria, usamos:
Quanto a e , podemos escrevê-los em função de , já que as relações entre eles são tabeladas. Olhando a tabela para Lapple:
Isolando e :
Jogando tudo isso na fórmula da vazão:
Agora, jogando tudo que temos na fórmula do , só vamos desconhecer o . O valor de é tabelada e, tendo uma equação e uma variável, achamos . Vou usar unidades do SI.
Calculando (repara que dá pra cortar um em cima e embaixo):
Usando a tabela, achamos todas as outras dimensões; por exemplo, como:
E ah! O enunciado pediu a vazão também, né? Como já achamos que:
Jogando o valor de :
Passo 5
Agora letra b: qual a potência de um soprador requerida, sendo a eficiência do soprador igual a 60%?
Falta só calcular a potência, mas antes disso, como:
Precisamos do . Falou de , lembra logo de Euler:
Só lembrando: esse no é a vazão que passa num ciclone apenas. Já o em é a vazão que passa pelo soprador, que vai ser o somatório das vazões que passam por ciclones em paralelo, caso existam. Nesse caso, só tem um ciclone então vão ser o mesmo valor.
é tabelado e a única coisa que não sabemos na expressão dele é o , daí:
Saiu em Pascal porque estou usando unidades do SI e essa é a unidade do SI pra pressão. A potência do soprador fica:
Resposta
- e