Um ciclone Stairmand HE de de diâmetro está tratando de ar a e 1 atm, contendo finos de ( e esfericidade 0,7). Devido a variações no processo industrial a granulometria do pó que chega ao ciclone aumentará em demasia. Desta forma, a fim de proteger o ciclone, será instalado um elutriador que deverá capturar todas as partículas maiores que , conforme o esquema abaixo.
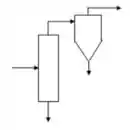
Pede-se:
a) Calcular o diâmetro do elutriador.
b) Calcular a eficiência global do processo.
Dado:
e
Passo 1
Nessa questão, temos equipamentos em série. Na letra a, estamos interessados apenas no elutriador, já na b, é pedida a eficiência do conjunto daí vamos ter que “dividir” o problema em 3:
- Achar a expressão de para o elutriador
- Achar a expressão de para o ciclone
- Achar a expressão de para o conjunto, usando:
Com sendo o elutriador e o ciclone.
Depois, é só integrar em , isto é, na entrada do equipamento , e acharemos a eficiência global, :
AHH! Uma coisa importante: o enunciado NÃO deu a densidade do gás, mas deu as condições dele
e 1 atm
Assumindo gás ideal, vale:
Podemos escrever o número de moles como , com sendo massa de gás e sendo a massa molecular média. Rearranjando:
Trabalhando no CGS e usando em Kelvin:
Passo 2
- Calcular o diâmetro do elutriador.
Nos foi informado que o elutriador deverá capturar todas as partículas maiores que . Daí, vamos analisar o limite, que é a partícula de . Para ela:
Daí, achando , achamos . Como:
Com sendo a vazão volumétrica e a área transversal do elutriador.
Poderemos achar o diâmetro do elutriador, já que temos
.
Para achar , EU VOU ASSUMIR que a partícula sedimenta na região de Stokes; vou assumir porque no elutriador só tem a força gravitacional e a partícula é pequenininha, mas depois tem que conferir, ok?
Pra região de Stokes vale:
Com
Como é dado que
Daí, trabalhando com o CGS e usando , já que só há força gravitacional no elutriador:
Massssss, antes de continuar, tem que conferir se, com essa velocidade, realmente está na região de Stokes. Fazemos isso calculando o Reynolds. Se você calcular, vai ver que dá:
E, com esse Reynolds, realmente está na região de Stokes! OK!
Se você não quisesse ir por esse caminho, poderia ter aplicado as correlações de Coelho e Massarani de cara.
Passo 3
Agora que temos , podemos calcular o diâmetro do elutriador:
Como vou usar o CGS, preciso converter :
Daí:
E lembrando que:
Passo 4
b) Calcular a eficiência global do processo.
Como já disse lá no passo 1, vamos ter que usar:
Daí bora começar pelo que já está meio caminho andado: o elutriador. Assumindo elutriador ideal, vale:
Como vamos, depois, ter que integrar em , bora expressar esses limites em termos de logo:
Para :
Daí:
Passo 5
Indo, agora, para o ciclone. A fórmula de é:
Novamente, bora começar pelo mais fácil? Haha Vamos integrar em , daí vamos ter que colocar em função de . Fazemos isso usando a fórmula dada para . E repara que não precisa mexer em porque ele é um número.
Agora, bora achar o . Fazemos isso usando o , que é tabelado. Para Stairmand HE:
E a fórmula pra é:
Usando o CGS e substituindo tudo que temos:
Então podemos escrever do ciclone como:
Passo 6
Agora é só juntar tudo.
Como é definido em 2 intervalos, vamos ter que dividir em 2 intervalos também:
- Para :
- Para :
Daí nossa integral também vai ser divida em 2 intervalos: