Deseja-se estudar o desempenho de uma bateria constituída por ciclones Lapple em série com respectivamente e de diâmetro no tratamento de de gás contendo em volume de sólido.
- Propriedades do gás: e
- Propriedades das partículas sólidas: e distribuição granulométrica dada por:
Pede-se:
- A eficiência global de coleta do sistema
- A potência do soprador para o serviço
Passo 1
Nessa questão, temos dois ciclones em série.
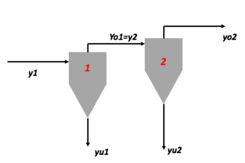
Tem uma vazão de gás “sujo”, a ser tratado, que passa pelo primeiro ciclone; um certo nível de separação ocorre e a vazão que sai desse primeiro ciclone vai, já mais “limpa”, para um segundo ciclone.
Sabemos que a vazão de alimentação é de . Como vou trabalhar no CGS, vou converter logo:
Essa vazão vai ser fixa nos dois ciclones, já que não há razão de fluido, isto é, as partículas saem puras, sem levar junto o fluido. Daí todo o fluido que sai de um ciclone vai para o outro. E, antes que você pergunte, eu sei que essa vazão não vai ser exatamente igual porque ela é a vazão de suspensão e a suspensão inclui partículas, que estão sendo parcialmente separadas. Mas repara que a concentração delas é baixa e não vai influenciar quase nada; é uma excelente aproximação dizer que é constante.
Agora, embora a vazão seja constante, o vai ser diferente em cada ciclone; esses ciclones são da mesma família e, para uma mesma família, é constante; acontece que o é diferente pra cada um deles e, por isso, a queda de pressão muda. Pra você visualizar melhor:
Pra finalizar essa introdução à questão, algo muitoooo importante: repara que ele dá a concentração volumétrica de partículas, que é . Embora essa concentração não seja tão importante no que diz respeito à vazão, vamos ter que considerar correção da velocidade terminal porque .
Passo 2
Para calcular a eficiência granulométrica global de equipamentos em série, temos que usar:
Em que é o do equipamento e é o do equipamento . Fisicamente, essa fórmula está nos dizendo que a separação granulométrica total é o que é separado no primeiro equipamento mais o que é separado do segundo , sendo que o que passa pela separação do segundo é só o que não foi separado no primeiro, daí o multiplicar por .
A expressão de ,para cada um dos ciclones, é:
E, como vimos na teoria, usamos o para obter o :
é tabelado e, de resto, na expressão, sabemos tudo menos . Daí equação e variável: solução única! Agora, vamos fazer assim: vamos, por um tempo, para o país das maravilhas com a Alice; enquanto a gente tiver lá, vamos fingir que não temos que corrigir a velocidade terminal e calcular para cada um dos dois ciclones; depois a gente volta pra realidade, ok? Vou chamar esses diâmetros de corte “imaginários” de . O é porque é relativo as condições de diluição infinita, sem efeito de concentração.
Para o primeiro ciclone:
Repara que eu passei a viscosidade de para , porque Poise que é a unidade do CGS pra viscosidade.
De forma semelhante, para o segundo ciclone:
Agora está na hora de voltar pra realidade. Um ciclone não separa as partículas por tamanho, quem faz isso é um filtro, por exemplo, mas, mesmo assim, nos referimos a DIÂMETRO de corte e não “alguma outra coisa” de corte; o ciclone separa partículas pela velocidade terminal delas, separa quando a partícula tem um tal que consegue bater na parede do ciclone antes de sair dele; sabemos relacionar diâmetro e e daí falar em diâmetros. Mas lembra disso: ciclone separa por velocidade.
Daí, para o primeiro ciclone, a só é chamada de diâmetro de corte porque tem uma tal que é separada com . Se tiver efeito de concentração, efeito extraterrestre, efeito de Júpiter ou qualquer outro (eu inventei estes dois últimos agora hein haha Não se assuta!), o ciclone não tá nem aí; ele continua na dele e a separação continua sendo por uma dada velocidade.
Acontece que, quando tem efeito de concentração, a velocidade terminal das partículas é alterada. Para o primeiro ciclone, por exemplo, precisamos achar qual é o diâmetro que nas condições de vai ter a mesma velocidade terminal da nas condições do país das maravilhas, ou seja, diluição infinita (concentração não afetando ), já que é a que amarra a separação.
Por esse último parágrafo, já sentiu um Coelho e Massarani no ar, né? Rs Bora lá! Temos um diâmetro, , e queremos a velocidade terminal dele nesse gás. Daí, vamos por:
Agora, pra achar o :
Precisamos de e ; como o enunciado não falou nada sobre esfericidade, vou assumir .
Calculando:
E, como isso tudo veio da condição de diluição infinita, esse é o :
Ok. Achando a dessa partícula:
Trabalhando com tudo no CGS:
Daí essa velocidade de é a “velocidade de corte”, a velocidade associada com . A questão agora é descobrir qual é o tamanho de partícula que, nas condições de , vai ter essa velocidade, ou seja, descobrir o tamanho de partícula associado a .
Passo 3
Para descobrir o tamanho de partícula associado a , vamos ter que fazer a correção “inversa” de concentração e descobrir a dessa partícula. Depois, relacionamos essa com diâmetro. Vem comigo que vai ficar tudo mais claro. A fórmula pra correção de concentração é:
Em que o valor de do é calculado de forma diferente dependendo do :
Com sendo o Reynolds calculado supondo que a esfera está isolada.
Calculamos o para a partícula e NÃO para essa real do equipamento com . Mas repara que achamos pra primeira , que é bem menor que . Vou assumir que esse novo vai, também, ser menor que e usar . Sim, esse é um caminho iterativo mas não tem muito por onde fugir; se chegar lá na frente e o for maior que , temos que voltar pra esse ponto...mas com uma folga dessas que temos, provavelmente não vai ser não.
Ok, aplicando:
Agora, temos uma velocidade e queremos saber o diâmetro correspondente:
Calculando
Oba! Reynolds menor que ! Não precisa voltar pra iterar. Bora continuar. Quem é o diâmetro que tem essa velocidade?
E, depois disso tudo, achamos o para o primeiro ciclone!
Fizemos isso tudo pro primeiro ciclone devido a nele. Para o segundo, será que precisa? Parte das partículas são separadas no primeiro então, talvez, seja menor que o segundo e não precisaremos corrigir. Então, guarda essa informação de para o primeiro ciclone e bora calcular a eficiência dele.
Passo 4
A fórmula de para ciclone é:
Para o primeiro ciclone, fica:
Para saber quanto de partículas foi separado no primeiro ciclone, não basta a eficiência por tamanho... precisamos da eficiência global, , que obtemos integrando de até , para varrer todos os diâmetros.
Como vamos integrar em , precisamos escrever em função de . Daí bora dar uma olhada na curva que o enunciado deu:
Manipulando:
Jogando em :
É nessa hora que a gente fica muito grato a quem inventou as calculadoras haha Calculando isso aí:
Agora, concorda comigo que as partículas que vão pro segundo ciclone são as que NÃO são separadas do primeiro, isto é, (? Então, chamando de a concentração volumétrica na entrada do ciclone e de a concentração volumétrica na entrada do segundo:
UFA! Como , não precisamos corrigir nada no segundo.
Passo 5
Escrevendo a expressão de para o conjunto:
Como o problema pede a eficiência global, temos que integrar:
Jogando esse monstro na calculadora:
Passo 6
b) A potência do soprador para o serviço
O pior já foi. Agora só falta a potência.
Como os ciclones estão em série: , porque a vazão que passa por um é a mesma que passa pelo outro...são as mesmas moléculas do fluido; passam por um e depois vão pro outro.
Temos que nos preocupar só com o , porque a queda de pressão total no sistema é a soma das quedas no primeiro e segundo.
Então, bora calculá-las! Temos que usar Euler, que é tabelado.
Para o primeiro ciclone:
Para o segundo:
Daí:
Como o enunciado não deu a eficiência do soprador, vamos ter que supor uma. Não me bate! É isso mesmo haha Vou supor . Daí:
Só pra ficar mais bonitinho, vou passar essa potência pra HP (horse power, ok? Não a calculadora haha)