Defeitos superficiais
Produzido por Erick PinhoTeoria
Faaaaaaala aí galera!!! Tudo certinho?
Falaremos agora sobre os defeitos superficiais. Mas afinal o quê é um defeito superficial?
São defeitos bidimensionais ou interfaciais que compreendem regiões do material com diferentes estruturas cristalinas e/ou diferentes orientações cristalográficas.
Superfície externa
A figura abaixo é a “fotografia” da superfície de um metal feita em um perfilómetro óptico e mostra a rugosidade da superfície.
Mas será que as superfícies externas dos sólidos são um tipo de defeito?
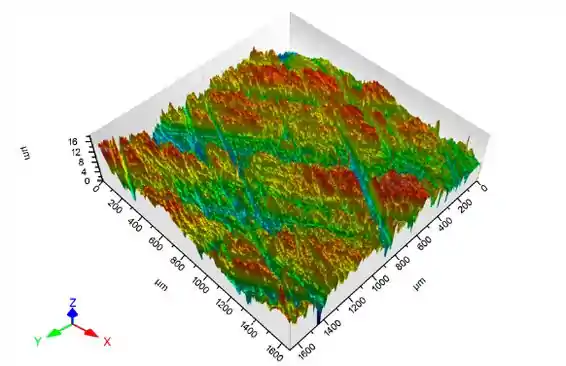
Para respondermos essa pergunta precisamos entender um pouco como são formadas as superfícies externas nos sólido.
Todo sólido possui um limite externo, que delimita sua superfície externa. Portanto, nessa superfície externa os átomos não estão completamente ligados, ou seja, existe ausência de ligações químicas.
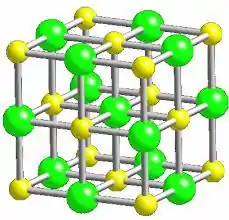
Suponham que a estrutura acima é um sólido com a forma de um quadrado. Notem que o átomo central está ligado a seis átomos ao seu redor. Suponham, também, que ambos os átomos, verdes e amarelos, satisfazem suas ligações com seis átomos. Logo, os demais átomos, localizados em torno do átomo central, não satisfazem por completo suas ligações químicas, isto é, não estão ligados a seis átomos vizinhos.

Como as ligações nas superfícies dos sólidos não são satisfeitas, estas superfícies estarão em um estado de energia mais elevado que os átomos do núcleo. Estas ligações insatisfeitas dos átomos da superfície dão origem a uma energia de superfície ou energia interfacial .
Tudo na natureza tende sempre a um estado de menor energia. É por esta razão, por exemplo, que uma gota de água tende à forma esférica, pois esta forma geométrica é a que possui o mesmo volume com a maior área superficial.

Além disso, a superfície externa pode ser bastante rugosa, conter pequenos entalhes e ser muito reativa quimicamente que o interior do cristal.
Contorno de fases
Os contornos de fase são as fronteiras que separam fases com estruturas cristalinas e composições distintas.
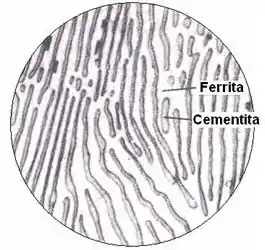
O esquema acima mostra uma microestrutura perlítica, onde vemos duas fases: cementita e ferrita.
Caaaaaalma! Não se preocupe com esses termos agora, pois os veremos mais tarde. O importante para agora é que você entenda que os contornos de fase, ou seja, a transição entre as duas fases é um tipo de defeito superficial e, também, possuem energias interfaciais diferentes dos seus núcleos.

Contorno de grão
Os contornos de grão, também, são defeitos interfaciais presentes em materiais policristalinos, que separam grãos (cristais) com diferentes orientações cristalográficas.
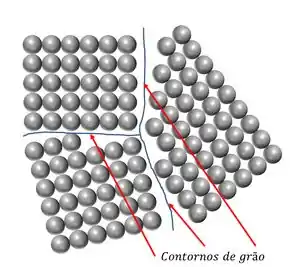
O esquema acima representa os contornos de grão, que são as interfaces que separam um arranjo de átomos como mesma orientação cristalográfica dos outros. Nota-se que o contorno de grão é uma área estreita na qual os átomos não estão à mesma distância uns dos outros. Em outras palavras, há átomos tão próximos em alguns pontos do contorno que causam tensão de compressão, ao passo que em outras áreas há átomos tão distantes que geram tensão de tração.
Nos materiais metálicos, os contornos de grão formam-se durante o processo de solidificação, quando os cristais, gerados a partir de diferentes núcleos, crescem simultaneamente e se encontram.

A figura acima mostra os contornos de grão reais de uma liga de cobre e níquel. Essa amostra foi polida e atacada quimicamente para posterior observação em microscópio óptico com um aumento de 500 vezes.
Como os contornos de grão são regiões de maior energia, portanto são regiões mais reativas quimicamente. Logo, uma amostra metálica, que foi polida e atacada quimicamente, terá os contornos de grão atacados mais intensamente que o restante dos grãos. Como os contornos foram mais atacados (corroídos) a luz emitida por um microscópio óptico sofrerá maior reflexão, assim observaremos regiões mais escuras.

Outra característica interessante dos contornos é que impurezas tendem a segregar (isolar-se) em seus entornos, a fim de diminuir a energia do contorno, como podemos observar na imagem acima da mesma amostra de liga de cobre e níquel, entretanto observada em microscópio eletrônico de varredura (MEV) com um aumento de 2000 vezes!!!!!
Em temperaturas muito elevadas os contornos de grão tendem a reduzir sua área, aumentando o tamanho médio do grão, com a finalidade de reduzir sua energia.
Podemos controlar as propriedades mecânicas de um metal ajustando o tamanho dos grãos, pois ao reduzirmos o tamanho dos grãos, aumentamos a quantidade total das áreas de seus contornos. Dessa maneira, qualquer discordância irá se mover apenas por uma curta distância antes de encontra o contorno e parar. Ao impedirmos a movimentação das discordâncias diminuindo o tamanho médio dos grãos e aumentando seus contornos, elevamos a resistência e dureza do material!!

Tamanho de grão
Vimos que o tamanho do grão é importante, já que a área de contornos de grão tem um efeito importante em algumas propriedades mecânicas dos metais, especialmente na resistência mecânica.
Como podemos medir esses tamanhos de grãos?

Para isso existem normas, por exemplo, ASTM, no qual se define o número de tamanho de grão , a partir da equação abaixo:
Em que é o número de grãos, por polegada quadrada, numa superfície polida e atacada, observada com uma ampliação de 100 vezes e , como dito anteriormente, é um número inteiro designado ASTM de tamanho de grão. Por exemplo, se observamos 128 grãos por polegada quadrada com um aumento de 100 vezes, nosso número de tamanho de grão será 8.
Vamos praticar?
Contorno de fases
Contorno de grão
Tamanho de grão
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercício FMS
Descreva o que são os contornos de grão.
Passo 1
Contorno de grão é uma região que separa dois ou mais cristais com orientações cristalográficas diferentes. Nessa região os átomos não estão a mesma distancia uns dos outros. Essas diferenças de distancias geram tensões, assim os contornos de grãos são regiões de maior energia.
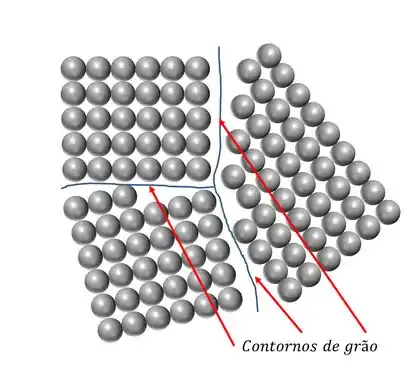
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Aponte na figura abaixo os defeitos. E separe-os em defeitos superficiais e pontuais.
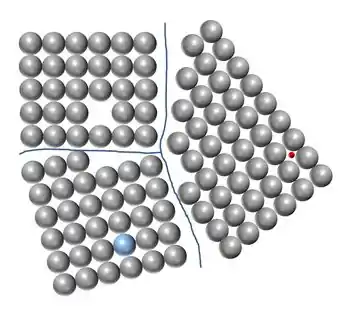
Passo 1
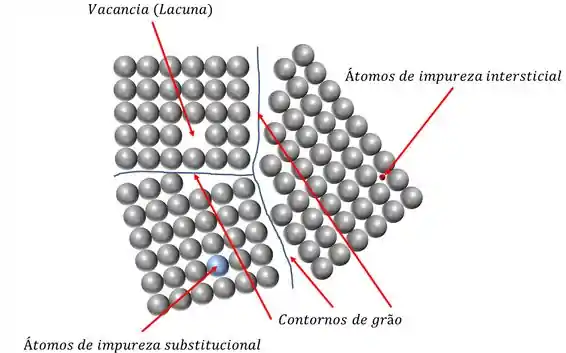
Passo 2
O defeito superficial é o contorno de grão. Já os defeitos pontuais são: átomos de impureza susbstitucional, átomo de impureza intersticial e lacunas.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Lista de exercício Unioeste
Um método de medida do tamanho de grão é o método ASTM, no qual se define o número de tamanho de grão como
Sendo , o número de grãos, por polegada quadrada, numa superfície do material, polida e contrastada, e é um inteiro designado número de ASTM de grrão.
- Uma micrografia observada com uma ampliação de 100X, apresenta número de tamanho de grão, . Quantos grãos por deveria ter essa amostra?
Passo 1
O que o problema nos pedi é quantos grãos por deveria ter essa amostra. Para isso basta substituir o tamanho de grão dado , na equação dada:
Logo, a amostra deveria ter 32 grãos por
Resposta
Exercício Resolvido #4
Lista de exercício Unioeste
Uma micrografia foi tomada de uma liga metálica com ampliação de 100X e da análise da mesma foi determinado um número médio de grão por igual a 10. Calcule o número de tamanho de grão ASTM para esta liga.
Passo 1
Para determinação do numero de tamanho de grão ASTM, utilizamos a seguinte equação:
Passo 2
O problema fornece o seguinte dado:
Passo 3
Agora vamos substituir o valor dado na equação ASTM:
Como o tamanho de grão deve ser um número inteiro, foi arredondado.
Resposta
Exercício Resolvido #5
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Determine o número do tamanho de grão ASTM para uma amostra metálica se são medidos 45 grãos por polegada quadrada, sob uma ampliação de 100X.
Passo 1
Para determinarmos o número do tamanho de grão ASTM, precisamos utilizar a equação abaixo:
Passo 2
O problema nos informa que foram medidos 45 grãos por polegada quadrada:
Passo 3
Agora devemos substituir o valor dado na equação:
Passo 4
Como o número do tamanho de grão ASTM deve ser um numero inteiro, logo
Resposta
Exercício Resolvido #6
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Determine o número do tamanho de grão ASTM se medidos 25 grãos por polegada quadrada sob uma ampliação de 600X.
Passo 1
Para ampliação diferentes de 100X devemos utilizar a seguinte equação:
Em que, é o numero de grão por polegada quadrada sob uma ampliação M.
Passo 2
Os dados do problema foram:
Passo 3
Agora é somente substituir os valores na equação:
Passo 4
Como o número de tamanho de grão deve ser um número inteiro, logo .
Resposta
Exercício Resolvido #7
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Determine o número do tamanho de grão ASTM se são medidos 20 grãos por polegada quadrada sob uma ampliação de 50X.
Passo 1
Para ampliação diferentes de 100X devemos utilizar a seguinte equação:
Em que, é o numero de grão por polegada quadrada sob uma ampliação M.
Passo 2
Os dados do problema foram:
Passo 3
Agora é somente substituir os valores na equação:
Passo 4
Como o número de tamanho de grão deve ser um número inteiro, logo .
Resposta
Exercício Resolvido #8
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Para um tamanho de grão ASTM igual a 8, aproximadamente quantos grãos devem existir por polegada quadrada:
- Para uma ampliação de 100X, e
- Sem qualquer ampliação?
Passo 1
Para determinação do numero de tamanho de grão ASTM, utilizamos a seguinte equação:
Passo 2
O problema fornece o seguinte dado:
Passo 3
Agora vamos substituir o valor dado na equação ASTM:
Passo 4
Para ampliação diferentes de 100X devemos utilizar a seguinte equação:
Em que, é o numero de grão por polegada quadrada sob uma ampliação M.
Passo 5
Os dados do problema foram:
Passo 6
Agora é somente substituir os valores na equação:
Resposta
Ei, a resposta está no passo a passo :)