Curva Tensão versus Número de ciclos (S-N)
Produzido por Erick PinhoTeoria
Fala aiiiiiiiiiiiiii pessoal!!!! Tudo tranquilo?
Vimos no tópico anterior que componentes submetidos a carregamentos cíclicos irão falhar em algum momento devido à fadiga. Mas que momento é esse?

Bom, para respondermos a essa pergunta precisamos entender o quê significa a curva tensão versus número de ciclos (Curva S-N), ou também conhecida como curva tensão versus vida.
A fim de determinarmos qual é o número de ciclos que o material suporta até a falha por fadiga realizamos ensaios laboratoriais ou ensaios de fadiga. Neste ensaio colocamos um corpo de prova submetido a um carregamento cíclico com amplitude de tensão (tensão alternada - ) ou tensão nominal conhecida até que o corpo de prova falhe por fadiga. No momento da falha verificamos qual é foi o número de ciclos que o material suportou. Esses ensaios, normalmente, são executados empregando tensão média nula ou uma tensão média especifica não nula .
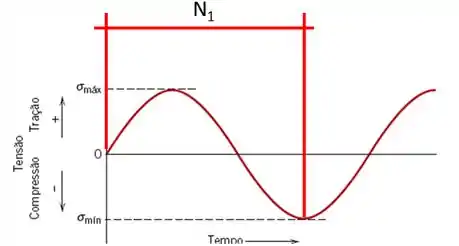
A figura acima nos mostra um carregamento cíclico completamente reverso, onde e . Imagine que esse gráfico representa o carregamento em nosso corpo de prova, além da tensão média e a amplitude de tensão, o gráfico nos mostra o primeiro ciclo de carregamento do material. Tanto a tensão média quanto a amplitude de tensão são escolhidas no inicio do ensaio. Já o número de ciclos até a falha iremos descobrir quando o corpo de prova falhar por fadiga. Esse número é dado pelo equipamento que realizamos o ensaio. O ensaio é repetido variando a amplitude de tensão (tensão alternada ) e verificando o número de ciclos até a falha que o material suportou. Como os valores das amplitudes de tensões e o número de ciclos até a falha traça-se um gráfico onde o eixo colocamos o número de ciclos até a falha e no eixo a amplitude de tensão, conforme figura abaixo.
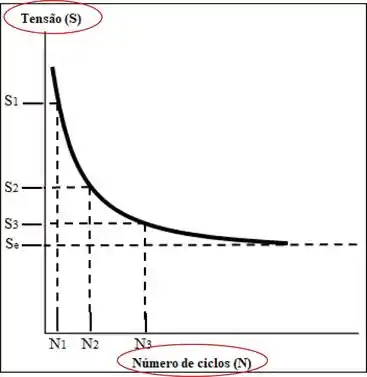
Note que apesar do número de ciclo até a falha está no eixo , ele é a variável dependente do ensaio e a amplitude de tensão ou tensão nominal a variável independente, uma vez que escolhemos cada tensão do ensaio.
O número de ciclos até a falha muda rapidamente com o nível de tensão e pode variar ao longo de várias ordens de grandeza. Por esse motivo, os números de ciclos são normalmente representados graficamente numa escala logarítmica. A figura abaixo mostra uma curva S-N com escala logarítmica no eixo dos números de ciclos.
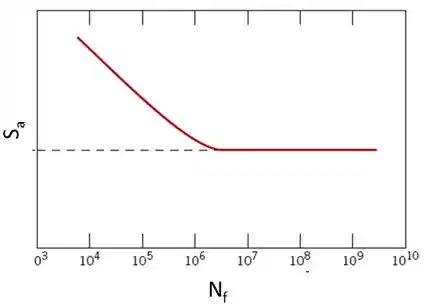
A equação que mais se aproxima do comportamento da curva S-N sem utilizar a escala logarítmica é uma equação potencial, conforme a equação abaixo.
Em que, é a amplitude de tensão ou a tensão nominal e B constantes e é o número de ciclos até a falha.
Em alguns materiais, notavelmente o aço-carbono comum e de baixa liga, parece haver um nível de tensão distinto abaixo do qual a falha por fadiga, praticamente, não ocorre em condições normais. Esse limite inferior de tensão é chamado limite de fadiga, isto é, abaixo desse limite de fadiga não há falha por fadiga em condições normais, ou pelo menos até onde foi medido o número de ciclos. Na verdade todo material irá sofrer falha por fadiga, mesmo que a tensão seja muito pequena, porém nesse limite de fadiga a variação é muitíssimo pequena e praticamente imperceptível.
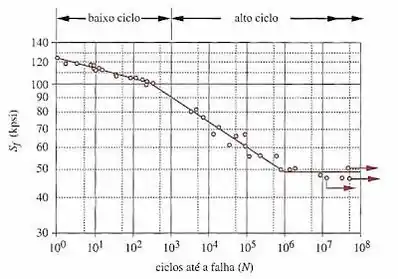
O termo resistência à fadiga é usado para especificar um valor de amplitude de tensão a partir de uma curva S-N para uma vida de particular interesse. Assim, a resistência à fadiga em é simplesmente a amplitude de tensão correspondente à . Outros termos usados com curvas S-N incluem fadiga de alto ciclo e fadiga de baixo ciclo. O primeiro identifica situações de longas vidas em fadiga em que a tensão é suficientemente baixa para que os efeitos da deformação plástica não ocorram. O número de ciclos em que a fadiga de alto ciclo inicia-se varia com o material, mas é tipicamente na faixa . Já para a fadiga de baixo ciclo temos deformação plástica e elástica causadas pelas cargas relativamente altas. Um bom exemplo de fadiga de baixo ciclo é a fratura de um clipe para papel, quando ao dobramo-lo demasiadamente algumas vezes, o quebramos. Note na figura acima a representação dessa classificação.

Tente ai quebrar um clipe por fadiga de baixo ciclo!!!!
E ai, vamos praticar?
Exercícios Resolvidos
Exercício Resolvido #1
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Um ensaio de fadiga foi conduzido de tal modo que a tensão média foi de e a amplitude de tensão foi de .
(a) Calcule os níveis de tensão máximo e mínimo.
(b) Calcule a razão entre as tensões.
(c) Calcule a magnitude do intervalo de tensões(faixa de tensões).
Passo 1
Vamos primeiramente anotar os valores dados e quais são os valores pedidos:
Valores dados:
Valores pedidos:
Passo 2
Vamos calcular agora os níveis de tensões máximo e mínimo. Sabemos que:
Isolando e substituindo:
Substituindo o valor de na equação abaixo:
Passo 3
Agora vamos calcular a razão de tensões:
Passo 4
Por fim, calculamos a magnitude do intervalo de tensões ou a faixa de tensões:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica, de aço 1045, que tem comportamento S-N conforme está apresentado na Figura abaixo, é submetida a ensaios giratórios com dobramento segundo ciclos alternados de tensões. Se o diâmetro da barra é de 15,0 mm, determine a carga cíclica máxima que pode ser aplicada para assegurar que não irá ocorrer uma falha por fadiga. Considere um fator de segurança de 2,0 e que a distância entre os pontos de aplicação de carga seja de 60,0 mm (0,0600 m).
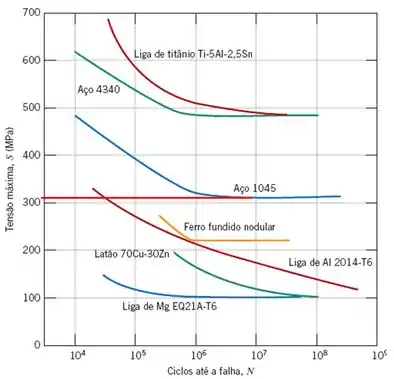
Passo 1
Observando a curva S-N acima nota-se que o limite de resistência à fadiga, portanto a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, .
Para calcularmos a tensão máxima e um componente sob flexão utilizamos a formula da flexão para barra redonda:
Em que é a força aplicada no ensaio, é o comprimento do corpo de prova e é o diâmetro do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando a força na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :
Resposta
Exercício Resolvido #3
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica em ferro fundido dúctil é submetida a ensaios giratórios com dobramento e alternados; os resultados dos ensaios (isto é, o comportamento S-N) estão mostrados na Figura abaixo. Se o diâmetro da barra é de 9,5 mm, determine a carga cíclica máxima que pode ser aplicada para assegurar que não irá ocorrer uma falha por fadiga. Assuma um fator de segurança de 2,25 e que a distância entre os pontos de suporte da carga seja de 55,5 mm.
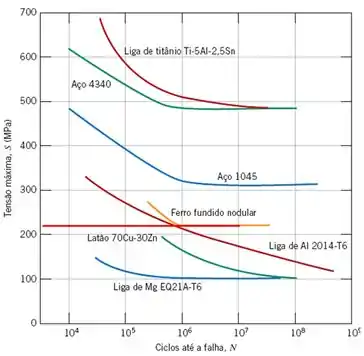
Passo 1
Observando a curva S-N acima nota-se que o limite de resistência à fadiga, portanto a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, , suponha que seja um carregamento com ciclo mínimo nulo:
Para calcularmos a tensão máxima em um componente sob flexão utilizamos a formula da flexão para barra redonda:
Em que é a força aplicada no ensaio, é o comprimento do corpo de prova e é o diâmetro do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando a força na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :
Resposta
Exercício Resolvido #4
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica em aço 4340 é submetida a ciclos de tensão giratórios com dobramento alternados, cujos resultados do ensaio estão apresentados na Figura abaixo. Se a carga máxima aplicada é de 5.000 N, calcule o diâmetro mínimo permissível para a barra para assegurar que não irá ocorrer uma falha por fadiga. Considere um fator de segurança de 2,25 e que a distância entre os pontos de suporte da carga seja de 55,5 mm.
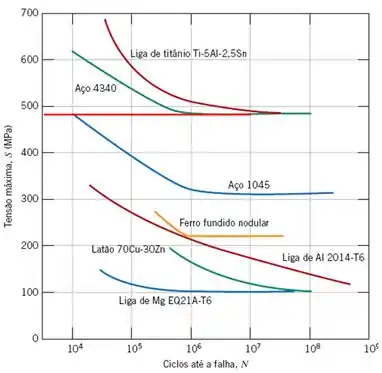
Passo 1
Observando a curva S-N acima nota-se que o limite de resistência à fadiga, portanto a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, , suponha que seja um carregamento com ciclo mínimo nulo:
Para calcularmos a tensão máxima e um componente sob flexão utilizamos a formula da flexão para barra redonda:
Em que é a força aplicada no ensaio, é o comprimento do corpo de prova e é o diâmetro do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando o diâmetro na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :
Para asseguramos que a barra não falhará por fadiga devemos arrendodar o valor do diâmetro para cima, pois se arrendodarmos para baixo a tensão máxima irá exceder o limite de resistência à fadiga. Assim:
Resposta
Exercício Resolvido #5
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica em liga de alumínio 2014-T6 é submetida a um ciclo de tensões de tração e de compressão ao longo do seu eixo; os resultados desses testes estão mostrados na Figura abaixo. Se o diâmetro da barra é de 12,0 mm, calcule a amplitude de carga máxima permissível (em N) para assegurar que não ocorrerá uma falha por fadiga em ciclos. Assuma um fator de segurança de 3,0, que os dados na Figura abaixo foram tomados a partir de ensaios alternados axiais de tração e de compressão, e que T seja a amplitude da tensão.
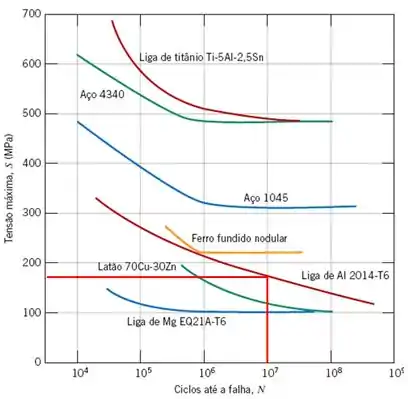
Passo 1
Observando a curva S-N acima para o ciclos até nota-se que a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, , suponha que seja um carregamento com ciclo mínimo nulo:
Para calcularmos a tensão máxima e um componente sob tensões axiais utilizamos a formula abaixo:
Em que é a força aplicada no ensaio e A é a área do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando a força na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :
Logo, a carga máxima permissível (em N) para assegurar que não ocorrerá uma falha por fadiga em ciclos é de:
Resposta
Exercício Resolvido #6
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica com 6,7 mm de diâmetro, fabricada a partir de uma liga de latão 70Cu-30Zn, é submetida a um ciclo de aplicação de cargas giratórias com dobramento; os resultados dos ensaios (na forma do comportamento S-N) estão mostrados na Figura abaixo. Se as cargas máxima e mínima são de +120 N e –120 N, respectivamente, determine a sua vida em fadiga. Considere que a distância de separação entre os pontos de suporte da carga seja de 67,5 mm.
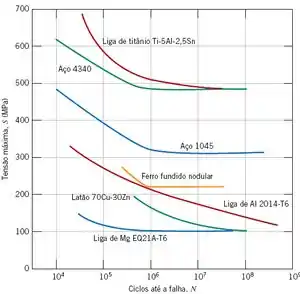
Passo 1
O problema nos fornece os seguintes dados:
Através da formula de flexão vamos calcular as tensões máxima e mínima(Obs.: Se deixarmos a força em e as medidas em obteremos a tensão em :
Passo 2
Vamos agora calcular a tensão alternada. Precisamos dessa tensão pois a curva S-N foi obtida através de ciclos de tensões alternadas. Outra coisa que temos que está atento e que o eixo , ciclos até a falha, , está em escala logarítmica.
Repare que quando tivermos forças ou tensões máximas e mínimas igual em modulo a tensão alternada é:
Como dito a tensão máxima está em função do logaritmo do número de ciclos até a falha por fadiga (), assim, traçado um reta na tensão até chegar na curva S-N do material, teremos o seguinte número de ciclos até a falha por fadiga:
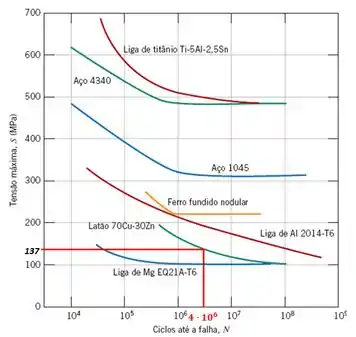
Resposta
Exercício Resolvido #7
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma barra cilíndrica com 14,7 mm de diâmetro, fabricada a partir de uma liga de titânio Ti-5Al-2,5Sn (Figura abaixo), é submetida a um ciclo de aplicação de cargas repetidas de tração e de compressão ao longo do seu eixo. Calcule as cargas máxima e mínima que deverão ser aplicadas para produzir uma vida em fadiga de ciclos. Assuma que os dados na Figura abaixo tenham sido tomados a partir de ensaios com cargas axiais repetidas de tração e de compressão, que a tensão indicada no eixo vertical seja a amplitude de tensão, e que os dados tenham sido obtidos para uma tensão média de 50 MPa.
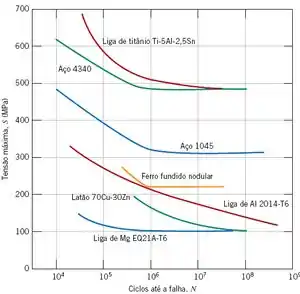
Passo 1
Observando a curva S-N acima para o ciclos até nota-se que a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, .
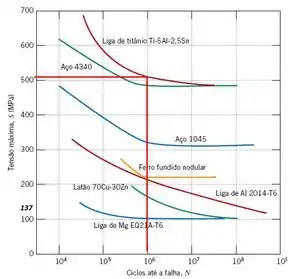
Para calcularmos a tensão e um componente sob tensões axiais utilizamos a formula abaixo:
Em que é a força aplicada no ensaio e A é a área do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Passo 2
Agora vamos obter os valores das cargas máximas e mínimas para isso vamos calcular as tensões máxima e mínima:
Passo 3
Sabemos que:
Assim, as cargas são:
Resposta
Exercício Resolvido #8
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Os dados de fadiga para um aço estão fornecidos a seguir.
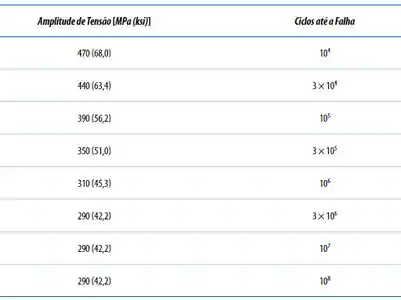
- Trace um gráfico S-N (amplitude da tensão em função do logaritmo do número de ciclos até a falha) usando esses dados.
- Qual é o limite de resistência à fadiga dessa liga?
- Determine as vidas em fadiga para as amplitudes de tensão de 415 MPa e 275 MPa.
- Estime as resistências à fadiga a e ciclos.
Passo 1
Primeiramente vamos pegar os pontos dados e traçar uma curva S-N. Lembre-se que no eixo estamos na escala logarítmica!
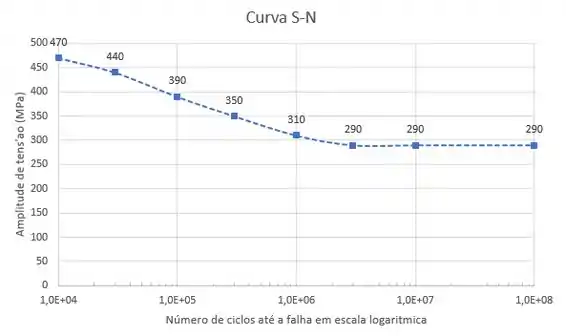
Passo 2
O limite de resistência a fadiga dessa liga é a tensão na qual a curva torna-se horizontal, que é de
Passo 3
Como podemos notar na curva abaixo, temos uma vida em fadiga para de aproximadamente ciclos e para teremos uma vida em fadiga infinita.
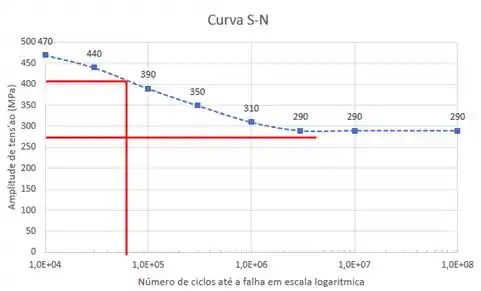
Passo 4
Traçando uma reta no eixo , vemos que a interseção com a curva S-N ocorrerá em:
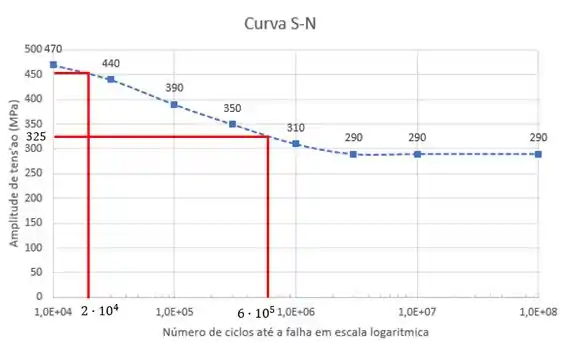
Resposta
Ei, a resposta está no passo a passo :)