Fluência
Teoria
E ai pessoal!!!! Tranquilo?
É comum material de engenharia estar submetido a condições de temperaturas elevadas e exposto a tensões mecânicas estáticas. Mas será que, caso o material esteja submetido a tensões abaixo do escoamento, pode sofrer uma falha?
A fluência é um tipo de falha que o material sofre quando está submetido a temperaturas elevadas, mesmo sobre tensões estáticas abaixo do escoamento.
A fluência é definida como: deformação permanente e dependente do tempo de materiais submetidos a uma carga ou tensão constante. Não desejamos que nossas peças falhem por fluência, portanto ao projetarmos um componente que estará submetido a altas temperaturas devemos considerar esse fenômeno, pois este é um fator limitante na vida útil de uma peça. Ela é observada em todos os tipos de materiais, porém para metais, ela se torna importante quando o mesmo trabalha em temperatura acima de 40% da temperatura absoluta de fusão do material.
Comportamento geral em fluência
Para determinarmos o comportamento do material em fluência submetemos o material em um ensaio de fluência. Esse ensaio consiste em aplicar uma tensão ou uma carga constante, ao mesmo tempo em que também se mantém a temperatura constante. Em um gráfico da deformação por fluência em função do tempo plotamos o comportamento do material.
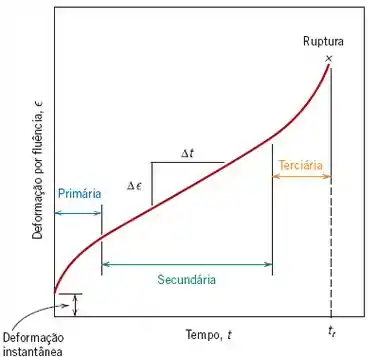
O gráfico acima mostra a deformação em fluência em função do tempo. Note que com a carga aplicada temos uma deformação elástica instantânea. Depois desta, vemos três regiões distintas da curva de fluência:
- Fluência primária: essa etapa é caracterizada por uma taxa de fluência continuamente decrescente, ou seja, temos a diminuição da deformação com o tempo. Essa diminuição sugeri que o material esteja aumentando sua resistência a fluência.
- Fluência secundária: nessa etapa temos uma taxa de deformação constante. Normalmente, esse estágio da fluência é o de maior duração. Essa taxa constante pode ser explicada pelo equilíbrio entre os processos de encruamento e recuperação.
- Fluência terciária: nessa temos uma aceleração da taxa até a ruptura do material.
Um dos parâmetros mais importante em um ensaio de fluência é a inclinação da porção secundária. Muitas vezes, essa inclinação é conhecida como taxa de fluência estacionária (). Ao projetarmos aplicações de longo prazo levamos em consideração essa taxa. Para aplicações onde os componentes possuem vidas relativamente curtas, o tempo para a ruptura, ou o tempo de vida até a ruptura , é a consideração de projeto predominante.
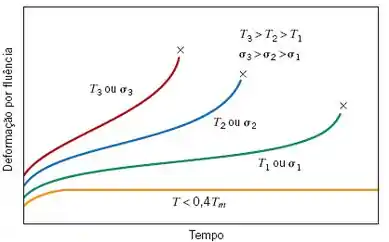
O gráfico acima mostra como a temperatura ou a tensão influenciam o comportamento em fluência do material. Note que em temperatura abaixo a , e após deformação permanente inicial, a deformação é independente do tempo. Com o aumenta da temperatura ou da tensão observe que: (1) a deformação elástica instantânea é aumentada; (2) a taxa de fluência estacionaria é aumenta e (3) o tempo de vida até a ruptura é diminuído.
Desenvolveram relações empíricas nas quais a taxa de fluência estacionária é expressa em função da tensão e da temperatura.
A equação acima demostra a relação da tensão com a taxa de fluência. Já a equação abaixo, tem-se a influencia da temperatura no processo.
Em que, , e são constantes do material. também é uma constante do material e é denominada energia de ativação para o processo de fluência.
Tivemos vários mecanismos teóricos propostos para explicar o comportamento da fluência. Esses mecanismos envolvem a difusão de lacunas induzida pela tensão, difusão nos contornos de grão, o movimento de discordâncias e o escorregamento do contorno de grão.
Muitas vezes, precisamos dos dados de fluência para uso prático na engenharia. Porém, para aplicações onde o tempo é dado em anos e como não é possível ensaiar o material pelo tempo real, uma solução para isso foi ensaiar o material em uma temperatura acima daquelas necessárias, por períodos de tempo mais curto e sob um nível de tensão comparável, para então fazer uma extrapolação dos dados para as condições de serviço. Um procedimento de extrapolação comumente utilizado é o parâmetro de Larson-Miller:
Em que é uma constante, para em Kelvin e o tempo de vida até a ruptura .
Fatores como temperatura de fusão, módulo de elasticidade e o tamanho de grão afetam o comportamento em fluência dos metais. Geralmente, quanto maior a temperatura de fusão, maior o módulo de elasticidade, e quanto maior o tamanho de grão, melhor a resistência do material à fluência. Grãos menores permitem maior escorregamento dos contornos de grão, resultando, assim, em maiores taxas de fluência.
Comportamento geral em fluência
Exercícios Resolvidos
Exercício Resolvido #1
Concurso UNIRIO – Engenheiro de Mecânico - 2016
Uma das propriedades dos materiais é a fluência que está relacionada à
- Medida da capacidade de um material de absorver energia até a fratura.
- Capacidade de um material absorver energia quando deformado elasticamente e, após o descarregamento, recuperar essa energia.
- Medida da capacidade de um material de resistir à formação de uma marca permanente quando pressionado por outro material.
- Medida da capacidade de um material em resistir a uma alteração estrutural permanente, progressiva e localizada, produzida por tensões e deformações cíclicas.
- Deformação plástica que ocorre em qualquer tipo de material, decorrente da aplicação de uma carga constante em função do tempo e, normalmente, a temperaturas elevadas.
Passo 1
Fluência é o nome dado a deformação plástica que o material sofre ao longo do tempo, quando submetido a uma carga ou tensão constante e a temperaturas elevadas.
Resposta
Letra: e)
Exercício Resolvido #2
Petrobras - 2011
Na seleção de aços para emprego em equipamentos de indústria petroquímica que operam em elevadas temperaturas (acima de 400ºC), qual é, tipicamente, a propriedade mais importante a ser observada?
- Temperabilidade
- Tenacidade à fratura
- Temperatura de transição dúctil – frágil baixa
- Resistência ao impacto
- Resistência à fluência
Passo 1
Aços submetidos a altas temperaturas, maiores do que 40% da temperatura de fusão do aço, sobrem deformação por fluência, assim na seleção desses materiais para trabalhar com alta temperaturas devemos observar a resistência à fluência desse material.
Resposta
Letra: e)
Exercício Resolvido #3
Elaboração própria
Quais são os três estágios da fluência?
Passo 1
Fluência é a deformação do material quando submetido a uma carga ou tensão constante ao longo do tempo. Para que o fenômeno ocorra a temperatura deve ser maior do que 40% da temperatura de fusão do material. Há três estágios na fluência:
- Estágio I: Nessa fase há um alongamento inicial instantâneo do material, na qual a velocidade de fluência diminui ao longo do tempo, isto é, a taxa de fluência diminui continuamente ao longo do tempo.
- Estágio II: Nessa fase a velocidade de fluência é praticamente constante, pois isso, essa fase é considerada como fluência estacionária.
- Estágio III: Nessa fase a velocidade de fluência aumenta rapidamente com o tempo até a deformação de fratura, ou seja, até a ruptura do material.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Explique o que ocorre em cada estágio de fluência.
Passo 1
Durante o estágio I ou fase primária o metal encrua até conseguir suportar a carga aplicada e a taxa de fluência diminui com o tempo, à medida que o encruamento torna a fluência (deformação) mais difícil, pois isso que nessa fase a velocidade de fluência diminui ao longo do tempo.
Passo 2
No decorrer do estágio II os processos recuperação envolvendo o movimento de discordâncias irá dificultar o encruamento do material, assim, a taxa de fluência constante nessa fase está relacionada ao equilíbrio entre os processos concorrentes de recuperação e encruamento. E nesse estágio onde teremos a menor taxa de fluência, também, a resistência a fluência do metal é máxima nesse estágio.
Passo 3
Ao longo do estágio III a taxa de fluência aumenta até a ruptura pois começa à estricção (empescoçamento) e, consequentemente, formação de cavidades particularmento no contornos de grão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
No ensaio de fluência, a taxa de deformação no estágio II é um dos parâmetros a serem obtidos. Pode-se dizer que essa taxa de deformação, também chamada de taxa de fluência,
- aumenta linearmente com o aumento do tempo.
- não varia com a tempo.
- aumenta exponencialmente com o aumento da tensão aplicada.
- não varia com a tensão aplicada.
- aumenta exponencialmente com o aumento do tempo.
Passo 1
No estágio II de fluência a taxa de fluência (deformação) é praticamente constante, isto é, há um aumento linear da deformação em relação ao tempo, conforme podemos notar na figura abaixo.
Resposta
Letra: a)
Exercício Resolvido #6
Elaboração própria
Qual é o efeito da temperatura sobre a fluência?
Passo 1
Para temperaturas abaixo de 40% da temperatura de fusão da liga, a liga apresentará uma deformação linear, mas a fluência secundária é insignificante, já que a temperatura é demasiadamente baixa para permitir a recuperação por difusão, isto é, após a deformação inicial não haverá deformação dependente do tempo, assim para temperatura abaixo de 40% da temperatura de fusão da liga não ocorrerá o fenômeno da fluência.
Já para temperaturas acima de 40% da temperatura de fusão da liga será observado o seguinte:
- A deformação instantânea no momento de aplicação da carga aumento aumenta com o aumento da temperatura;
- A taxa de fluência estacionária aumenta com o aumento da temperatura;
- O tempo de vida do material até a ruptura diminui com o aumento da temperatura.
O gráfico abaixo representa a tensão em função do tempo de vida até a ruptura, ambos em escala logarítmica. Note que para uma mesma tensão aplicada quanto maior a temperatura menor será o tempo de vida do material.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria
De acordo com o gráfico abaixo, qual é o efeito da tensão aplicada e da temperatura sobre a taxa de fluência estacionaria?
Passo 1
Para mesma temperatura da liga, note que a taxa de fluência aumenta com o aumento da tensão aplicada e, consequentemente, com o aumento da taxa de fluência teremos uma diminuição da vida até a ruptura do material, conforme podemos observar na figura abaixo.
Note que com o aumento da temperatura para uma mesma tensão aplicada teremos um aumenta da taxa de fluência estacionária, conforme figura abaixo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Enade - 2008
A resistência mecânica dos metais pode ser reduzida com o aumento da temperatura de ensaio. Tendo em vista que a mobilidade dos átomos aumenta com a temperatura, pode-se concluir que processos controlados por difusão têm efeito significativo nas propriedades mecânicas a temperaturas elevadas.
Materiais expostos a tensões em altas temperaturas, como, por exemplo, rotores de turbinas de aeronaves, linhas de vapor de alta pressão e paredes de reatores nucleares, sofrem deformações permanentes dependentes do tempo, denominadas fluência. Ensaios de fluência são realizados em altas temperaturas para caracterização mecânica a quente dos materiais.
Considerando a curva típica de fluência apresentada na figura abaixo, assinale a opção correta.
- A constância da taxa de fluência na fase secundária está relacionada ao equilíbrio entre os processos concorrentes de encruamento e recuperação.
- Ensaios de fluência por compressão são mais apropriados para materiais dúcteis, pois, nesse caso, existirão amplificações de tensão e propagação de trincas.
- Os parâmetros mais importantes do ensaio são as inclinações da porção terciária, conhecidas como taxas mínimas de fluência.
- O parâmetro de Larson-Miller permite a determinação do mecanismo predominante para um material específico.
- O aumento da temperatura ou do nível de tensão no ensaio de fluência promove a redução da deformação inicial instantânea e o aumento no tempo de vida até a ruptura.
Passo 1
A taxa de fluência constante no estágio II é devido aos processos de recuperação em equilíbrio com o processo de encruamento do material.
Resposta
Letra: a)