(a) Compare as densidades planares (Seção e Problema ) para os planos (), () e () da estrutura cristalina CFC.

(b) Compare as densidades planares (Problema ) para os planos (), () e () da estrutura cristalina CCC.

(b) Para a estrutura cristalina do CCC, as densidades planares dos planos e foram determinadas no Problema da seguinte maneira:

Agora, compararemos com o plano (, o qual é mostrado dentro de uma célula unitária CCC na Figura (a) a seguir.

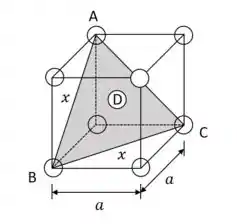
Figura (a)

Os centros dos três átomos nas arestas, denotados por A, B e C, estão neste plano. Além disso, o plano não passa pelo centro do átomo D, localizado no centro da célula unitária. O empacotamento atômico deste plano é apresentado na Figura (b) a seguir; as posições correspondentes do átomo da Figura (a) também são observadas.

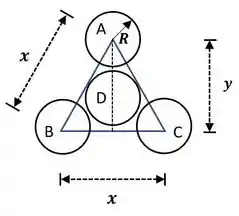
Figura (b)

Como esse plano não passa pelo centro do átomo D, ele não é incluído na contagem de átomos. Um sexto de cada um dos três átomos identificados como A, B e C está associado a este plano, o que equivale a meio átomo.

Na Figura (b), o triângulo tendo A, B e C como arestas é um triângulo equilátero. E, na Figura (b), a área desse triângulo é . O comprimento da borda do triângulo, , é igual ao comprimento de uma face na diagonal, conforme indicado na Figura (a). E seu comprimento está relacionado ao comprimento da borda da célula unitária, , da seguinte forma:

Então, para CCC, (Equação - pág. 41; 8ª Ed.), e, portanto,

Além disso, da Figura (b), com relação ao comprimento , podemos escrever:

O que leva a

E a substituição do valor de , como mostra a expressão anterior, produz:

Assim, a área deste triângulo é igual a

E, finalmente, a densidade planar para o plano é: