Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 53

Considerando os dados representados na Figura 6.19 , especifique equações, semelhantes às Equações 6.20 a e 6.20 b para os aços, que relacionem o limite de resistência à tração e a dureza Brinell para o latão e o ferro fundido nodular.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom... podemos especificar estas equações a partir da análise da Figura 6.19 :

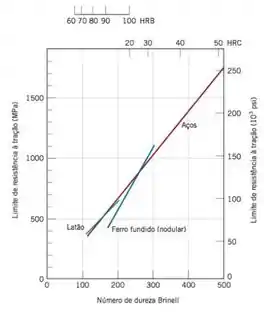
Podemos considerar que as retas são da forma:

T S = a H B + b

Onde a e b são constantes. Vamos descobrir estas constantes!!!

Passo 2

Para o latão temos que:

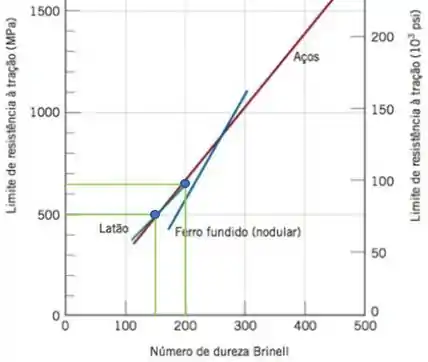
Ou seja, para:

T S = 500 → H B = 150

T S = 650 → H B = 200

Portanto, substituindo as equações, temos que:

500 = a 150 + b

650 = a 200 + b

Subtraindo a primeira equação da segunda, temos que:

650 - 500 = 200 a - 150 a + b - b

150 = 50 a

a = 3

Se a = 3 , substituindo na primeira, temos que:

500 = 3 150 + b

b = 500 - 450

b = 50

Portanto a equação geral para o latão é:

T S M P a = 3 H B + 50

Passo 3

Para o ferro fundido nodular temos que:

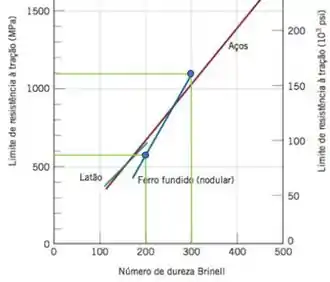
Ou seja, para:

T S = 5 9 0 → H B = 20 0

T S = 1100 → H B = 3 00

Portanto, substituindo as equações, temos que:

5 9 0 = a 20 0 + b

1100 = a 3 00 + b

Subtraindo a primeira equação da segunda, temos que:

110 0 - 5 9 0 = 3 00 a - 20 0 a + b - b

510 = 10 0 a

a = 5,1

Se a = 5,1 , substituindo na primeira, temos que:

5 9 0 = 5,1 20 0 + b

b = 5 9 0 - 1020

b = - 430

Portanto a equação geral para o ferro fundido nodular é:

T S M P a = 5,1 H B - 430

Resposta

Para o Latão:

T S M P a = 3 H B + 50

Para o Ferro Fundido Nodular:

T S M P a = 5,1 H B - 430

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dez quilogramas de polibutadieno são vulcanizados com 4.8kg de enxofre. Qual fração dos possíveis sítios para ligações cruzadas está ligada por pontes de enxofre, assumindo que, na média, 4.5 átomos d
Para a vulcanização do poli-isopreno, calcule a porcentagem em peso de enxofre que deve ser adicionada para assegurar que 8% dois sítios possíveis formem ligações cruzadas; considere que, na média, tr
O limite de resistência à tração e a massa molar numérica média para dois polietilenos são os seguintes:Estime a massa molar numérica média necessária para produzir um limite de resistência à tração d
Para cada um dos seguintes pares de polímeros, trace e identifique em um mesmo gráfico as curvas esquemáticas tensão-deformação [isto é, trace gráficos separados para os itens (a), (b) e (c) ].Polipro
A partir dos dados de tensão-deformação do poli (metil metacrilato) mostrados na Figura 15.3, determine o módulo de elasticidade e o limite de resistência à tração à temperatura ambiente [20 ° C (68 °