Demonstre que a razão mínima entre os raios do cátion e do ânion para um número de coordenação de vale .

Esse problema nos pede para mostrar que a relação mínima de raio cátion/ânion para um número de coordenação de é . A partir da célula da unidade cúbica dada por

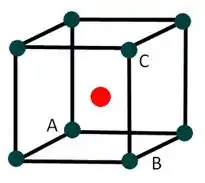
Onde o lado no nosso quadrado mede (duas vezes o raio do ânion). Temos que o comprimento de vai ser a diagonal da face, assim, por Pitágoras teremos

Agora, vamos utilizar o triângulo e aplicar Pitágoras no mesmo a fim de encontrarmos finalmente a relação entre os raios, assim, vamos ver

Mas se repararmos na nossa figura temos que , substituindo na equação acima vamos encontrar

Tirando a raíz quadrada em ambos os lados e desconsiderando a raíz negativa que não convém, vamos encontrar

Dividindo todo mundo por vamos encontrar

Como nós desejávamos mostrar.