Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 12.Perguntas e Problemas - Ex. 2
Mostre que a razão mínima entre os raios do cátion e do ânion para um número de coordenação de vale .
Passo 1
Neste problema, nos é pedido que mostremos que a razão mínima entre os raios do cátion (íon positivo) e o ânion (íon negativo) para um número de coordenação vale . Temos que para um número de coordenação vamos ter a disposição de um tetraedro que pode ser muito bem inscrito em um cubo de lado de tal forma que podemos fazer a seguinte construção
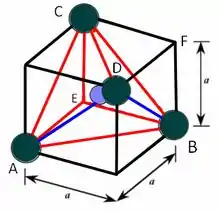
É válido lembrar aqui que reduzimos o tamanho das esferas para ficar mais fácil a visualização. Pois bem, temos que o cátion reside no centro do nosso cubo e, além disso, vamos designar por os raios do cátion e do ânion, respectivamente. Como o comprimento é uma diagonal da face do cubo temos que
Mas, como na realidade os átomos todos estão se tocando vamos podemos expressar como sendo
Fazendo a igualdade entre as duas expressões nós vamos conseguir escrever o lado do nosso cubo em função do raio do ânion da seguinte forma
Passo 2
Bom, não podemos esquecer que também haverá um ânion localizado na esquina, ponto (não desenhado), e a diagonal do cubo estará relacionada aos raios iônicos como
Respira, estamos quase acabando. Se a gente reparar no triângulo formado percebemos que é possível aplicar Pitágoras de tal forma que obteremos o seguinte
Mas, da nossa construção geométrica temos que e, ainda, . Dessa forma, vamos ter o seguinte
Dividindo todo mundo por 2 vamos encontrar
Agora, vamos dividir todo mundo por obtendo, assim,
Que é uma equação do segundo grau cujas raízes são dadas por
Nesse caso, podemos desconsiderar a raíz negativa pois não nos convém e ficaremos com
Como queríamos mostrar.