Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 6
Mostre que o fator de empacotamento atômico para a estrutura HC é de 0,74.
Passo 1
O fator de empacotamento atômico é a razão entre o volume de átomos na célula unitária dividido pelo volume da célula unitária. Na a estrutura HC (hexagonal compacta), o número de átomos dentro da célula unitária é átomos, como pode ser observado nas figuras abaixo:
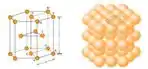
A gente também consegue ver que os átomos estão todos encostadinhos, logo .
Passo 2
Para calcular o volume atômico, calculamos como sendo o volume da esfera:
Para calcular o volume da célula unitária, calculamos a área do hexágono vezes a altura.
E temos, tabelado, que:
Então:
E como
Passo 3
Finalmente, pra gente chegar no FEA, a gente precisa tirar a razão entre eles!
Resposta
, como queríamos demonstrar!
Exercícios de Livros Relacionados
Para um composto cerâmico, quais são as duas características dos íons que os compõem, as quais determinam a estrutura cristalina?
Quais dos cátions da Tabela 12.3 você estima que forme iodetos com a estrutura cristalina do cloreto de césio? Justifique suas escolhas.
Mostre que a razão mínima entre os raios do cátion e do ânion para um número de coordenação de 6 vale 0,414 . (Sugestão: use a estrutura cristalina do N a C l (figura 12.2 ) e assuma que os ânions e c
A estrutura cristalina da blenda de zinco pode ser gerada a partir de planos compactos de ânions. a A sequência de empilhamento para essa estrutura será C F C ou H C ? Por quê? b Os cátions ocuparão p
Demonstre que a razão mínima entre os raios do cátion e do ânion para um número de coordenação de 8 vale 0,732 .