Mostre que a razão mínima entre os raios do cátion e do ânion para um número de coordenação de vale . (Sugestão: use a estrutura cristalina do (figura ) e assuma que os ânions e cátions apenas se tocam ao longo das arestas do cubo através das diagonais das faces.)

Para resolvermos esse problema vamos utilizar a sugestão dada no próprio enunciado que é de usar a estrutura do a qual podemos planificar obtendo a seguinte estrutura

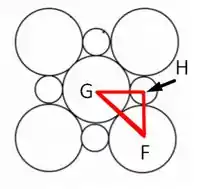
Se denotarmos por os raios do cátion e ânion, respectivamente, podemos reparar que

Além disso, temos que

No triângulo destacado em vermelho na imagem podemos aplicar Pitágoras de forma que vamos obter

Aplicando a raíz quadrada em ambos os lados (desconsiderando a parte negativa que não nos convém) vamos ter

Dividindo todo mundo por vamos encontrar

Pronto, está mostrado o que a questão queria.